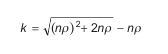NCMA tek 14-19B

[struct_eeyore]

For those of you who are familiar with this TEK... Link here
I'm a bit embarrassed to say this, but I cannot for the life of me confirm the values in the tables for the closer spaced bar conditions.
For example, if I take the 8" o.c. #8 centered in cells, I get a masonry stress controlling condition that's about 12000 in-lb/ft less than the table (3.a)
For the fully grouted condition I treating each 8" cell as a rectangular beam, and calculating masonry moment with (Fb/2)(jkbd^2).
If I work the provided moments backwards thru this formula, I get Fb = 1718 (~ f'm 3800!).
What am I doing wrong here? Were these tables calculated using strength design, and reduced backwards into ASD? Can the discrepancy be this large?

 

[DaveAtkins]

I only use strength design for CMU. My guess is #8 @ 8" would not be allowed for strength design, because the wall would be over-reinforced.

DaveAtkins

 

[XR250]

I can't imagine it being OK for ASD. The CMU would surely fail way before the steel.

 

[JLNJ]

Some of those tables show the reinforcement offset from the center of the wall.

I would be hesitant to do this with a single layer of bars. The field guys are too used to centered bars and the arrangement would be prone to error.

 

[XR250]

I usually show offset (for retaining walls) but design for center

 

[Celt83]

The tables are ASD, for table 3a, 8" block with #8 @ 8:
h,nominal = 8 in
h = 7.625 in
tf = 1.25 in, face shell thickness
f'm = 1500 psi
As = 0.79 in^2
s = 8 in
b,eff = min(s, 6*h,nominal, 72) = 8 in
d = h / 2 = 3.8125 in
n = Es/Em = 900*f'm / 29000000 = 21.4815
rho = As/(b,eff d) = 2*As / (b,eff*h) = (2*0.79) / (8*7.625) = 0.025
n*rho = 0.5564
k = 0.63623
j = 1 - (k/3) = 0.7879
Mmsy = [Fb*(k*j*b,eff*d^2)] / 2 = [0.45*f'm*(k*j*b,eff*d^2)] / 2 = 19673.67 in-lbs, where Fb = 0.45 * f'm is the allowable stress in the masonry.
Msteel = 32000 * As * j * d = 75939.79 in-lbs

Mr = min(Mmsy, Msteel) = 19673.67 in-lbs

Convert Mr to be per ft width of wall:
Mr,1 ft = Mr / (b,eff / 12) = Mr / (8/12) = 29510.51 in-lbs/ft (table value 29511 in-lbs/ft)

 

[StrEng007]

I'm typically designing slender walls and use SD to incorporate the secondary effects (P-delta) on the wall. The #8 at 8" o.c. seems futile to me.

That being said, I'd need to brush up on the ASD procedures for walls. I don't recall there being an upper limit to the vertical reinforcing used for flexure.

 

[XR250]

I'm not sure I have seen an upper limit. i just put enough in so the masonry fails first.
I might add extra if I am not confident in the grouting procedures.

 

[DaveAtkins]

i just put enough in so the masonry fails first.

Shouldn't we design so that the steel fails before the masonry? A ductile failure?

DaveAtkins

 

[struct_eeyore]

Celt - I'm with you all the way till the k calc - can you explain in more detail?

 

[Celt83]

For the 8" o.c. spacing the wall ends up solid grouted so the formula for k should be based on a rectangular section:

 

[struct_eeyore]

Welp, that solved it. My one hardcover reference had swapped + to -... Your time is much appreciated.