Tmoose,
What exactly are you trying to show there? I assume this is the shift drum along which the shift forks in a transmission ride or something similar and that you are referring to the grooves in which the shift forks ride.
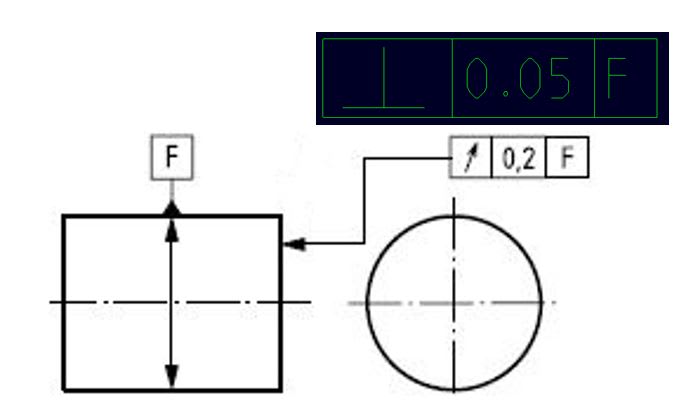
I'm fairly confident in my previous statement, and pmarc's confirmation solidifies that for me. The statement applied to a nominally flat surface which mirror's the OP's question. The surface you have introduced is not nominally flat, and I don't think surface perpendicularity/orientation makes sense on a feature which is not flat (no provisions per Y14.5 or Y14.5.1 for such an specification), perpendicularity applied to a cylindrical/width-shaped feature (or perhaps more generally - a feature which has a UAME aka FOS from which an axis/centerplane can be derived) would imply axis/centerplane perpendicularity at RFS (or surface if MMC is applied to the same type of feature) - your only option for the feature you have shown (approximately helical) would be perpendicularity of EACH ELEMENT.
If we assume you mean to compare the perpendicularity of EACH ELEMENT on the surface of the grooves to circular runout, I don't think you could apply circular runout to these grooves. Circular runout (and really total runout - this can be debated as theres no example of it, but the Y14.5.1 math standard definition is broad enough) can indeed be applied to profiles other than the nominally cylindrical and flat (ie: conical) but at least for circular runout the definition is pretty clear that such a feature must be able to be derived circular elements from the nominal geometry (cylindrical symmetry aka n-fold rotational symmetry where n=infinity). For total runout I'm less clear on whether the part must have cylindrical symmetry - certainly for "surfaces constructed at a right angle to the datum axis" only covers features which are nominally flat as per Y14.5.1-1994 section 6.7.2 "all points of the surface must lie in a zone bounded by two parallel planes perpendicular to the datum axis and separated by the specified tolerance" which would suggest only nominal planar features. To me the shape you presented would fall under "constructed at a right angle to the datum axis" and would thus be excluded as it is not nominally flat. If one were to try and cover it under 6.7.3 "Surfaces Constructed Around a Datum Axis" I'm not as certain - my gut says no but I'm interested in alternate views.
I think you're comparing apples and oranges anyway - even with a nominally flat surface perpendicularity of EACH ELEMENT would not be equivalent to perpendicularity of the entire surface, and definitely not to circular/total runout of said surface.