How delta t is Calculated in Abaqus Explicit?

[Mechanicslearner]

Hello Abaqus users,
Does anyone know how Δt in Abaqus explicit is calculated?. I tried Δt = l/c but that is stable increment. I would like to know how velocity is calculated in Abaqus explicit so I need Δt values . I even added screenshot of the formula. If it is based on natural frequency then delta t values does not vary much but it does vary alot. Please someone help me with this.

 

[Dave442]

The calculation of the stable time increment in explicit is described in the theory manual:

Abaqus Theory Guide -> Procedures -> Explicit dynamic analysis -> Stability

 

[Mechanicslearner]

Hello Dave442,

I read those formulas but it still not to my understanding or I am using wrong formulas for natural frequency. Please have a look at my values for cantilever beam with axial load at tip and only one linear element is used for ease of understanding.

I already read the thread (

http://www.eng-tips.com/viewthread.cfm?qid=311561)

before. 5th comment from bottom where henki says ///" BUT when I calculated the "I" in transverse direction, the time step size decreased to 8E-8s. This seems to determine the time step size, even though this latter stiffness has no effect on the results. I ran the beam analysis again using a fixed time increment of 1E-6s and the results were same as those obtained with 5E-8s. So this answers my question."///

Does this mean I have to calculate transverse moment of inertia instead second moment of inertia for natural frequency? if so what is formula for rectangular cross section as I could not find it, am sorry to say that.

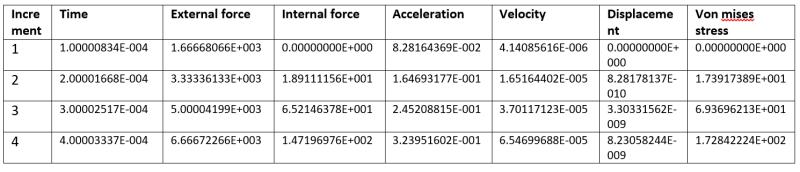
Please read the short explanation of how I got the delta t(i+1) and delta t(i) values by using increment 1 and increment 2 values from above table:
Increment 1:
acceleration = 0.0828164369 m/sec^2, velocity = 0.00000414085616 m/sec, displacement = 0 (dont know why its zero)
according to Abaqus Theory guide 2.4.5 (

http://129.97.46.200:2080/v6.14/books/stm/default....)

velocity(i+0.5) = velocity(i-0.5) + [((delta t(i+1) + delta t(i))/2) * acceleration(i)]
so substituting increment 1 value gives
0.00000414085616 = 0 +[((delta t(i+1) + delta t(i))/2) * 0.0828164369]
(delta t(i+1) + delta t(i))/2) = 0.0000500004

Increment 2:
acceleration = 0.164693177 m/sec^2, velocity = 0.0000165164402 m/sec, displacement = 8.28178137*E-10
by using above method
(delta t(i+1) + delta t(i))/2) = 0.0000751433

but in this we have displacement value which makes it possible to get delta t(i+1) value from following equation
displacement(i+1) = displacement(i) + delta t(i+1)* velocity(i+0.5)
8.28178137*E-10 = 0 + delta t(i+1) * 0.0000165164402
delta t (i+1) = 0.0000501427
so delta t (i) = 0.0001001439

I know its amateur method of finding it but I did it to make sure what could be the values because Explicit does not do iterations so correct me if I am wrong in doing above calculation.

Now according to documentations:
delta t = L/c where c = sqrt(E/rho)
delta t = 2/omega , where omega is natural frequency
delta t = 2/omega * (sqrt(1+ ξ^2) - ξ) , where ξ is fraction of critical damping where I used default linear and quadratic bulk viscosity 0.06 and 1.2 respectively

from Roark's formula
omega = 1.732/2*pi * (sqrt(E*I*g/Wl^3)) because am trying to learn cantilever with axial load at tip with density = 8050 , poissons ratio = 0.33 , elasticity = 210 GPa , I know values are approximate for learning
I get closer to delta t values only by using roark's formuals, if there is any other formula for calculating natural frequency of cantilever beam let me know

I know this is a long reply but I typed to make it clear and I hope its easy for you guys to find delta t values. So please let me know if there is a correct natural frequency formula or alternative way for that and working on this for a week now

 

[Mustaine3]

The theoretical formula for the stable time increment is based on the highest eigenfrequency. How do you want to calculate that analytically (or numerically efficient)?

 

[Mechanicslearner]

Hello Mustaine3,

I have read that stability limit is based on highest eigen frequency, where it should be less than that highest frequency value. I have also read from this thread (

http://www.eng-tips.com/viewthread.cfm?qid=330104)

that Abaqus takes factor of those frequencies, not really sure about the factor numbers (0.9, 0.65, 0.7) . My question is how abaqus get those increment values based on which formula for eigen frequency ( or natural frequency)? Is it in a range of values to make the convergence , if so how the range is determined?

 

[Mustaine3]

The eigenfrequencies are not used. The estimation is based on the wave speed and the element size.

 

[Mechanicslearner]

Hello Mustaine3,

Thanks for the quick response. I already have tried using characterstic length (Le) to dilational speed wave ratio (cd) but the numbers are far from delta values.

Please see the following delta t values using various formulas:

1) delta t = L/C where L is element length which 10 metres in my case and C = sqrt(E/density) for beam which gives 0.00195789 for every increment as displacement is very small as you can see from table

2) delta t = L/c , where c equals sqrt((lambda+2*mu)/density) , which gives 0.0016084819

If there is anyother formula for dilational wave speed please let me know


omega = 0.2 * (sqrt(g/deflection)) , 0.2 used for cantilever instead of 1.732 which gives 0, 0.00009187, 0.0001835332, 0.0002897043 which has a range almost close to delta t values at the start but not as increment proceeds.

It would be very helpful if I know which formula is used, so I can learn how explicit really works. I guess we all can.