Hello Dave442,
I read those formulas but it still not to my understanding or I am using wrong formulas for natural frequency. Please have a look at my values for cantilever beam with axial load at tip and only one linear element is used for ease of understanding.
I already read the thread (
before. 5th comment from bottom where henki says
///" BUT when I calculated the "I" in transverse direction, the time step size decreased to 8E-8s. This seems to determine the time step size, even though this latter stiffness has no effect on the results. I ran the beam analysis again using a fixed time increment of 1E-6s and the results were same as those obtained with 5E-8s. So this answers my question."///
Does this mean I have to calculate transverse moment of inertia instead second moment of inertia for natural frequency? if so what is formula for rectangular cross section as I could not find it, am sorry to say that.
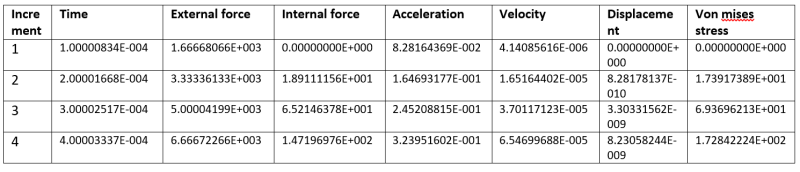
Please read the short explanation of how I got the delta t(i+1) and delta t(i) values by using increment 1 and increment 2 values from above table:
Increment 1:
acceleration = 0.0828164369 m/sec^2, velocity = 0.00000414085616 m/sec, displacement = 0 (dont know why its zero)
according to Abaqus Theory guide 2.4.5 (
velocity(i+0.5) = velocity(i-0.5) + [((delta t(i+1) + delta t(i))/2) * acceleration(i)]
so substituting increment 1 value gives
0.00000414085616 = 0 +[((delta t(i+1) + delta t(i))/2) * 0.0828164369]
(delta t(i+1) + delta t(i))/2) = 0.0000500004
Increment 2:
acceleration = 0.164693177 m/sec^2, velocity = 0.0000165164402 m/sec, displacement = 8.28178137*E-10
by using above method
(delta t(i+1) + delta t(i))/2) = 0.0000751433
but in this we have displacement value which makes it possible to get delta t(i+1) value from following equation
displacement(i+1) = displacement(i) + delta t(i+1)* velocity(i+0.5)
8.28178137*E-10 = 0 + delta t(i+1) * 0.0000165164402
delta t (i+1) = 0.0000501427
so delta t (i) = 0.0001001439
I know its amateur method of finding it but I did it to make sure what could be the values because Explicit does not do iterations so correct me if I am wrong in doing above calculation.
Now according to documentations:
delta t = L/c where c = sqrt(E/rho)
delta t = 2/omega , where omega is natural frequency
delta t = 2/omega * (sqrt(1+ ξ^2) - ξ) , where ξ is fraction of critical damping where I used default linear and quadratic bulk viscosity 0.06 and 1.2 respectively
from Roark's formula
omega = 1.732/2*pi * (sqrt(E*I*g/Wl^3)) because am trying to learn cantilever with axial load at tip with density = 8050 , poissons ratio = 0.33 , elasticity = 210 GPa , I know values are approximate for learning
I get closer to delta t values only by using roark's formuals, if there is any other formula for calculating natural frequency of cantilever beam let me know
I know this is a long reply but I typed to make it clear and I hope its easy for you guys to find delta t values. So please let me know if there is a correct natural frequency formula or alternative way for that and working on this for a week now