I have an existing structure I'm analyzing and I'm just not matching something. It's a parking deck, live load = 40 psf. Beam is 20" wide x 26" deep, pan joist system is 6" side x 18" deep with 4" slab (6" x 14" + 4" slab). The Beam span is 57' and the tributary width is 28'. The effective prestress force is 350 kips. At the center of the beam positive auxiliary rebar consists of 2#5 and 2#6 bars. At the support negative auxiliary rebar consists of 3#7 and 2#8 bars. I'm getting a capacity of 712 k-ft positive and 872 k-ft negative. I am getting a DEMAND of 630 k-ft positive and 1262 k-ft negative. This can't be right. I'm just checking the existing loads, I haven't put the proposed loads or anything on there. d=23.75". I'm not sure what I'm missing, I may be burnt out and missing something to simple that I may be booted from the forum but any help would be greatly appreciated.
Tek-Tips is the largest IT community on the Internet today!
Members share and learn making Tek-Tips Forums the best source of peer-reviewed technical information on the Internet!
-
Congratulations TugboatEng on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
Existing Post tension beam doesn't meet what the existing loads would require 4
- Thread starter jplay2519
- Start date
rapt said:
What you've presented is a simplified, alternate formulation of ultimate flexural capacity wherein the balancing load effect IS considered explicitly, correct? If so, then yes, it would be a salient example of the point that I've been trying to make.
I've been trying to come up with a version of this myself but was unsure of some aspects of it.
I would describe this formulation as the ultimate capacity calculated from the view of the prestressing effects as external loads. I do recognize that it's not as computationally expedient as the usual formulation of course. And I'm not proposing it as a replacement, just an illustrative example.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
ingenuity said:
I know. Similar statements pervade the literature. It wasn't my intention to single yours out.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
@Ingenuity: it was taken from one of those VSL manuals that I linked above. The slabs one I think. In light of my work and some of rapt's comments, I now take that to mean that one could calculate ultimate capacity using balancing loads but it would be a computational nightmare as a result of the influence of hyperstatic effects etc.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
Google tells me that it was from the first of the four VSL papers KootK linked above
Surprisingly, an exact search on Google finds a couple of other (possibly dodgy) sites with that paper, but not the VSL site.
Doug Jenkins
Interactive Design Services
See attached two PDF files related to this topic of equivalent loads due to prestress and ultimate strength.
The first paper is from the ACI Journal from 1985, authored by Waller and Zimmerman.
The second file is a discussion of the authors paper by Ken Bondy and Prof Mattock questioning the authors logic.
Evidently the authors original paper was not peer-reviewed before it was published!
The first paper is from the ACI Journal from 1985, authored by Waller and Zimmerman.
The second file is a discussion of the authors paper by Ken Bondy and Prof Mattock questioning the authors logic.
Evidently the authors original paper was not peer-reviewed before it was published!
Kootk,
Don't start suggesting that my post in any way justifies your logic. I was asking if that was what you were suggesting, not suggesting that it was a logical solution. I do not consider this to be a logical solution to ultimate strength calculations of PT members.
I think your position and the logic I asked about above shows complete lack of understanding of prestressed concrete analysis and design concepts.
Looking at the same example at midspan and using the same variables and simplified logic in it, and considering it as a strain compatibility exercise (except for the force in unbonded PT tendons)
M*midspan = (P + deltaP) * (e + D/2 - dc) (basically Tension force * lever arm)
This applies at any cross-section in the member and in any member, no matter how complex the section shape, the tendon profile and everything else.
If you break that down, there is a term in the right side which is P . e which is the initial PT contribution to the ultimate strength. But you cannot substitute Mp in there because in an indeterminate member, Mp includes secondary prestress as well, it is not just P.e . Also, there is a deltaP . e term that is completely missed in the earlier logic. THis increase in the prestress force also occurs in unbonded tendons but to a lesser degree due to the lack of strain compatibility. You could substitute Mp - Msec for P.e but why would you want to, as that Mp - Msec = P.e.
But this method allows the designer to calculate curvatures, strain compatibility between materials (other than unbonded PT), ductility effects etc. It is a logical way to estimate the ultimate capacity (or any) of a PT cross-section and also the moment curvature relationship throughout the loading range of a PT cross-section, from transfer to ultimate capacity. Something that is very useful for deflection calculations of cracked PT members.
To take this one step further, in the deflection calculations in RAPT, a service condition check, the balanced load and its effects are not used as they cannot be used in a cracked section check. It is all based on curvatures and curvatures are based on moment/curvature relationships, something you cannot do using your logic.
Even in Ingenuity's post above which suggests that it illustrates very well the effects of the service state, I would qualify to consider only the hypothetical/uncracked service state. It gives not assistance in crack control calculations or deflection calculations, both of which are Service State.
Don't start suggesting that my post in any way justifies your logic. I was asking if that was what you were suggesting, not suggesting that it was a logical solution. I do not consider this to be a logical solution to ultimate strength calculations of PT members.
I think your position and the logic I asked about above shows complete lack of understanding of prestressed concrete analysis and design concepts.
Looking at the same example at midspan and using the same variables and simplified logic in it, and considering it as a strain compatibility exercise (except for the force in unbonded PT tendons)
M*midspan = (P + deltaP) * (e + D/2 - dc) (basically Tension force * lever arm)
This applies at any cross-section in the member and in any member, no matter how complex the section shape, the tendon profile and everything else.
If you break that down, there is a term in the right side which is P . e which is the initial PT contribution to the ultimate strength. But you cannot substitute Mp in there because in an indeterminate member, Mp includes secondary prestress as well, it is not just P.e . Also, there is a deltaP . e term that is completely missed in the earlier logic. THis increase in the prestress force also occurs in unbonded tendons but to a lesser degree due to the lack of strain compatibility. You could substitute Mp - Msec for P.e but why would you want to, as that Mp - Msec = P.e.
But this method allows the designer to calculate curvatures, strain compatibility between materials (other than unbonded PT), ductility effects etc. It is a logical way to estimate the ultimate capacity (or any) of a PT cross-section and also the moment curvature relationship throughout the loading range of a PT cross-section, from transfer to ultimate capacity. Something that is very useful for deflection calculations of cracked PT members.
To take this one step further, in the deflection calculations in RAPT, a service condition check, the balanced load and its effects are not used as they cannot be used in a cracked section check. It is all based on curvatures and curvatures are based on moment/curvature relationships, something you cannot do using your logic.
Even in Ingenuity's post above which suggests that it illustrates very well the effects of the service state, I would qualify to consider only the hypothetical/uncracked service state. It gives not assistance in crack control calculations or deflection calculations, both of which are Service State.
A bit late perhaps, but I think there are a few points based on the "Golden Gate Bridge" analogy that are worth making:
Taking KootK's section B version of the GGBA:
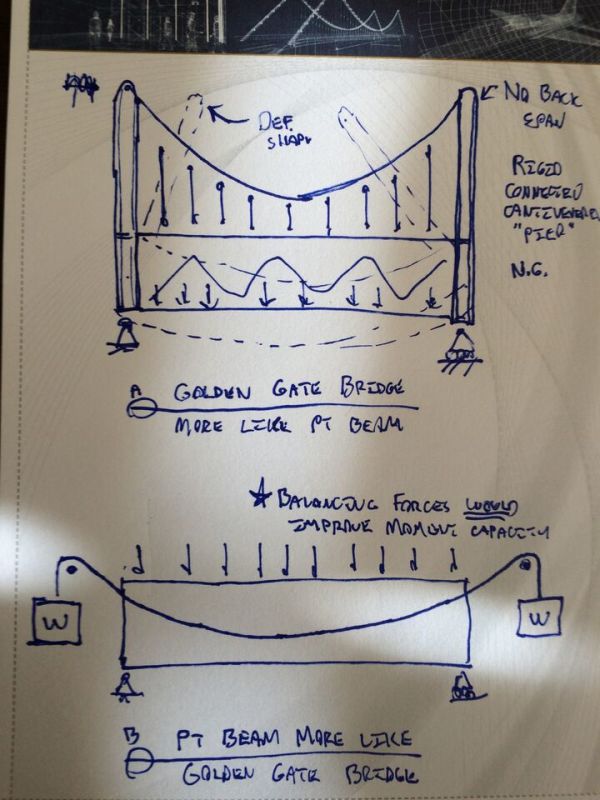
Let's make it even closer to an unbonded p-t beam by moving the cables down at the ends so they intersect at the concrete centroid, then anchor the cables to the concrete with a loss-free anchoring system. The forces in the cable are now the same, and the concrete is the same except it now has a uniform compressive stress.
Compare this with a beam with the same layout except it has horizontal bonded prestress with an Infinite Debonding System (patent applied for) so that at any section the stress in the concrete under dead load is exactly uniform.
At mid-span the stresses will be exactly the same in both systems. This applies to both the concrete and the cables.
As we move away from mid-span:
[ol 1]
[li]The force in the cables in the horizontal bonded system progressively reduces, so that the compressive stress in the concrete also reduces, but remains uniform.[/li]
[li]The shear forces are carried entirely through the cable in the unbonded system (as the vertical component of the cable force), and entirely through the concrete in the bonded system.[/li]
[/ol]
If we now apply an increasing uniform load until the maximum compressive strain in the concrete at mid-span reaches 0.003 (or whatever our ultimate limit strain is):
[ol 1]
[li]In the unbonded system the force in the cable will remain approximately unchanged (assuming sections at the end rotate about the concrete centroid, and ignoring the effect of increased sag), but at mid span there will be an increased moment due to the non-uniform concrete stress.[/li]
[li]In the bonded system the cable force will increase to yield, so the force in the concrete and the nett moment will both be higher than for the unbonded system.[/li]
[li]In both systems all the additional shear forces will pass through the concrete.[/li]
[/ol]
For the unbonded system we could calculate the ultimate moment as the sum of the balanced moment plus the additional moment in the concrete, but it is simpler just to work on the basis of force and moment equilibrium, as we would for the bonded system.
Doug Jenkins
Interactive Design Services
Taking KootK's section B version of the GGBA:
Let's make it even closer to an unbonded p-t beam by moving the cables down at the ends so they intersect at the concrete centroid, then anchor the cables to the concrete with a loss-free anchoring system. The forces in the cable are now the same, and the concrete is the same except it now has a uniform compressive stress.
Compare this with a beam with the same layout except it has horizontal bonded prestress with an Infinite Debonding System (patent applied for) so that at any section the stress in the concrete under dead load is exactly uniform.
At mid-span the stresses will be exactly the same in both systems. This applies to both the concrete and the cables.
As we move away from mid-span:
[ol 1]
[li]The force in the cables in the horizontal bonded system progressively reduces, so that the compressive stress in the concrete also reduces, but remains uniform.[/li]
[li]The shear forces are carried entirely through the cable in the unbonded system (as the vertical component of the cable force), and entirely through the concrete in the bonded system.[/li]
[/ol]
If we now apply an increasing uniform load until the maximum compressive strain in the concrete at mid-span reaches 0.003 (or whatever our ultimate limit strain is):
[ol 1]
[li]In the unbonded system the force in the cable will remain approximately unchanged (assuming sections at the end rotate about the concrete centroid, and ignoring the effect of increased sag), but at mid span there will be an increased moment due to the non-uniform concrete stress.[/li]
[li]In the bonded system the cable force will increase to yield, so the force in the concrete and the nett moment will both be higher than for the unbonded system.[/li]
[li]In both systems all the additional shear forces will pass through the concrete.[/li]
[/ol]
For the unbonded system we could calculate the ultimate moment as the sum of the balanced moment plus the additional moment in the concrete, but it is simpler just to work on the basis of force and moment equilibrium, as we would for the bonded system.
Doug Jenkins
Interactive Design Services
rapt said:
I must apologize then. I did not mean to taint your previous statements by associating them with my amateurish logical fumblings.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
IDS said:
Here's a version from VSL's site: [URL unfurl="true"]http://www.vsl.net/sites/default/files/vsl/datasheet/PT_Slabs.pdf[/url]
Ingenuity said:
I still can't access it...
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
IDS said:
I'm not clear with regard to what has been retained of the GGB analogy? This mostly sounds like an ordinary PT beam to me. Can you elaborate?
IDS said:
This sounds as though you may be agreeing with one of my recent assertions, namely that an alternate formulation of ultimate moment capacity could be developed using balancing load effects. If I'm out to lunch here, please don't be offended by my suggesting that you might agree with me.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
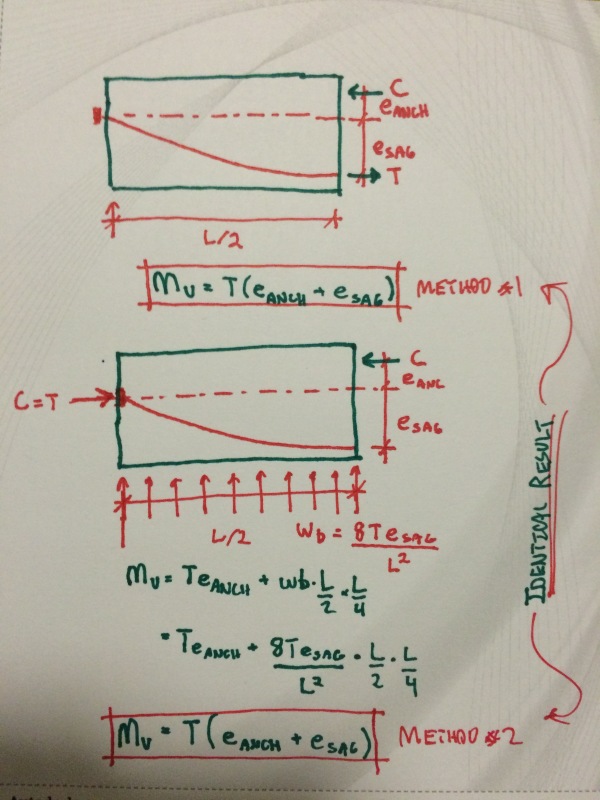
Sometimes I wonder if it appears as though I'm trying to lay claim to something more radical than I actually am. In an effort to clarify, please see the sketches below where I have derived the ultimate moment capacity of a simple plan post-tensioned beam:
a) Using the traditional approach.
b) Using the balanced load effect.
The algebra comes out in the wash and, as expected, the results are the same. Did I make a bunch of simplifying assumptions? You bet. And if you feel that any of those simplifying assumptions invalidates the core work, feel free to jump up and down while waving your arms furiously.
Here is a list of what I believe the takeaways are and are not:
1) Once could calculate Mu using the balancing load effect rather than the traditional method.
2) I am NOT suggesting that this is a better way to calculate Mu. It's a worse way computationally.
3) If one removed the balancing load effect from the second formulation below, the ultimate moment capacity would obviously be reduced. Since methods one and two are statically equivalent, the same is true for method one. Thus, balancing load effects play a role in ultimate moment capacity.
4) In the usual formulation, we don't get to apply T at (e_anch + e_sag) from C because that's where the tendon is. We get to apply T there because that's the location that the balancing load effect has shifted the center of precompresson to. It's just math/physics fun that the center of precompression is always located at the tendon height. I derived this aspect of things with details A&B above.
That's it. That's the entirety of my argument here.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
a) Using the traditional approach.
b) Using the balanced load effect.
The algebra comes out in the wash and, as expected, the results are the same. Did I make a bunch of simplifying assumptions? You bet. And if you feel that any of those simplifying assumptions invalidates the core work, feel free to jump up and down while waving your arms furiously.
Here is a list of what I believe the takeaways are and are not:
1) Once could calculate Mu using the balancing load effect rather than the traditional method.
2) I am NOT suggesting that this is a better way to calculate Mu. It's a worse way computationally.
3) If one removed the balancing load effect from the second formulation below, the ultimate moment capacity would obviously be reduced. Since methods one and two are statically equivalent, the same is true for method one. Thus, balancing load effects play a role in ultimate moment capacity.
4) In the usual formulation, we don't get to apply T at (e_anch + e_sag) from C because that's where the tendon is. We get to apply T there because that's the location that the balancing load effect has shifted the center of precompresson to. It's just math/physics fun that the center of precompression is always located at the tendon height. I derived this aspect of things with details A&B above.
That's it. That's the entirety of my argument here.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
KootK said:
What I have retained is everything except the cable is now anchored to the concrete, rather than an external point. The forces in the cable are exactly as before, and the bending and shear stresses in the concrete are exactly as before, i.e. zero. The only thing that has changed is that the concrete now has a uniform compression. The fact that the beam is now an ordinary PT beam is the point. The other point is that the stress distribution at mid-span is exactly the same as for a bonded post-tensioned system with the same cable profile, or a straight profile.
Doug Jenkins
Interactive Design Services
Kootk,
I was not going to respond again on this topic, but after reading your 4 points above, I think it is necessary
Answering your 4 points above
1 Yes, the calculations will work this way if
- the stress in the tendon at ultimate is the working stress - it is not
- the stress in the tendon is constant along it full length - it is not though it is sometimes assumed to be by lazy designers and lazy software developers
- the member is determinate
- the tendons are anchored at the centroid of the section at the ends
- the member is prismatic (there are no changes in section along its length)
- there are no reversal load situations
- the tendon has a single profile shape (no reverse curves etc)
- if you are only interested in an Ultimate capacity and nothing else (ductility, curvature etc) stresses and strains in other reinforcing in the section, compression reinforcement effects and anything else to do with section design. You cannot even determine the strength reduction factor for some design codes because it is related to strains and curvature (ACI and AS codes).
- probably a few others I have not thought of
2 see 1!
3 See 4!
4 The centroid of the tension force is not determined by the balanced load. T is at the centre of the tendon force which is at the centre of the tendon. The "equivalent balanced load effect" is caused by the drape in the tendon from the anchorage to its low point. Not the reverse.
Load Balancing is a calculation tool and that is all it is!
I was not going to respond again on this topic, but after reading your 4 points above, I think it is necessary
Answering your 4 points above
1 Yes, the calculations will work this way if
- the stress in the tendon at ultimate is the working stress - it is not
- the stress in the tendon is constant along it full length - it is not though it is sometimes assumed to be by lazy designers and lazy software developers
- the member is determinate
- the tendons are anchored at the centroid of the section at the ends
- the member is prismatic (there are no changes in section along its length)
- there are no reversal load situations
- the tendon has a single profile shape (no reverse curves etc)
- if you are only interested in an Ultimate capacity and nothing else (ductility, curvature etc) stresses and strains in other reinforcing in the section, compression reinforcement effects and anything else to do with section design. You cannot even determine the strength reduction factor for some design codes because it is related to strains and curvature (ACI and AS codes).
- probably a few others I have not thought of
2 see 1!
3 See 4!
4 The centroid of the tension force is not determined by the balanced load. T is at the centre of the tendon force which is at the centre of the tendon. The "equivalent balanced load effect" is caused by the drape in the tendon from the anchorage to its low point. Not the reverse.
Load Balancing is a calculation tool and that is all it is!
rapt said:
Don't put yourself out on my account. I've got access to most of the Australian Concrete Mafia on this thread. I'm sure that others can chip in if you find yourself otherwise indisposed.
You're likely to find my responses to your responses (below) quite unsatisfying. I apologize for that but really don't know what to do about it. Your statements are just that, statements. You don't seem to feel compelled to back them up with anything resembling proof or physical reasoning.
You've posted over 2000 words in this thread and, to date, not a single sketch. Not one. I suppose you figure that, with you being a PT deity and me being a hapless neophyte, I should just accept your statements as indisputable fact. Unfortunately, if I took that approach, I wouldn't learn a damn thing. And I'm here to learn.
rapt said:
KootK said:
If you don't understand why I've taken some simplifications, you are missing the point of the exercise.
rapt said:
We assume that the stress in the tendon is at ultimate level when we calculate ultimate bending capacity the usual way. I fail to see why that same strategy wouldn't work here.
rapt said:
Again, this is true with the usual formulation and the problem is surmountable. I don't see why it wouldn't work here.
rapt said:
I disagree. Some additional things would need to be considered in the formulation but, again, that is true of the conventional formulation as well.
rapt said:
I disagree. My derivation assumed indeterminate anchorage placement and seems to work just fine.
rapt said:
I disagree. You could take my derivation, change the profile of the bottom of the member any which way, and the result would be the same.
rapt said:
Load is just load. I fail to see why a change in direction should neuter the method.
rapt said:
You can calculate balanced load effects at serviceability with complex tendon layouts. I fail to see why it should be any different for the ultimate state.
rapt said:
KootK said:
If you think that this is about proposing a better computational method, you are missing the point of the exercise.
rapt said:
Load balancing is a computational tool and the load balancing effect is a real, physical phenomenon present at all stages during the life of a PT member. What more could you possibly ask of a concept? I fail to see how this is a limitation.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
KootK said:
We're the CIA, not the Mafia.
But personally I tend to say what I think, rather than based on the country of origin of whoever I am responding to.
On this particular thread, I'm not even sure what the point of contention is now.
Doug Jenkins
Interactive Design Services
hokie66 said:
hokie66 said:
I've been wanting to circle back to these statements. I initially found the first shocking and the second somewhat confusing. Having had some time to ruminate on this stuff, however, I think that I have some new insights that I'd like to have vetted.
First, a little background. On my first PT project, my mentor gave me his spiel about how tendon drape essentially allowed one to move load from the point of application out to the supporting columns without really involving the concrete. I thought it was super cool. And I still do. So when I found out that drape doesn't improve ultimate bending capacity, I was peeved.
Here's what I've come up with since:
1) Given a particular tendon elevation, drape does not improve cross section ultimate moment capacity. It may, however, improve member/structure ultimate load carrying capacity. This was probably what you intended all along with respect to the two statements quoted above.
2) In detail #1 below, I've considered a simple span beam in which the tendons are set out flat. In detail #2, I've considered the same beam with harped tendons. In a sense, one could say that even this member is improved by tendon drape as the draped arrangement reduces the flexural demand on the concrete at all sections other than midspan.
3) In detail #3, I've considered a continuous beam in which the tendons are draped to more optimal effect. In truly continuous members, one is afforded the opportunity to maximize tendon sag while still keeping anchorage forces located at the section centroid. This would seem to be an improvement over the simple span beam scenario.
4) To some extent, even simple span pre-stressed concrete members can exhibit features of continuity. This is because such members are effectively able to have applied end moments as a result of the pre-stress anchorage forces.
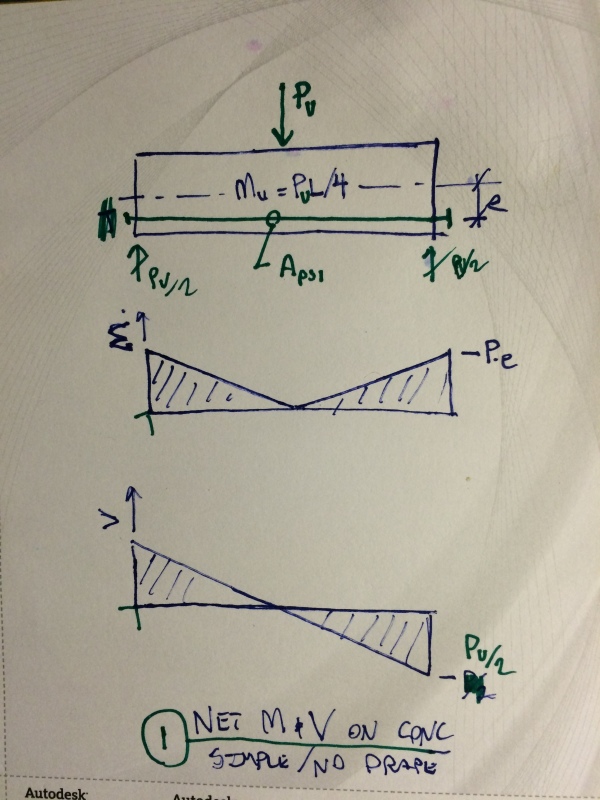
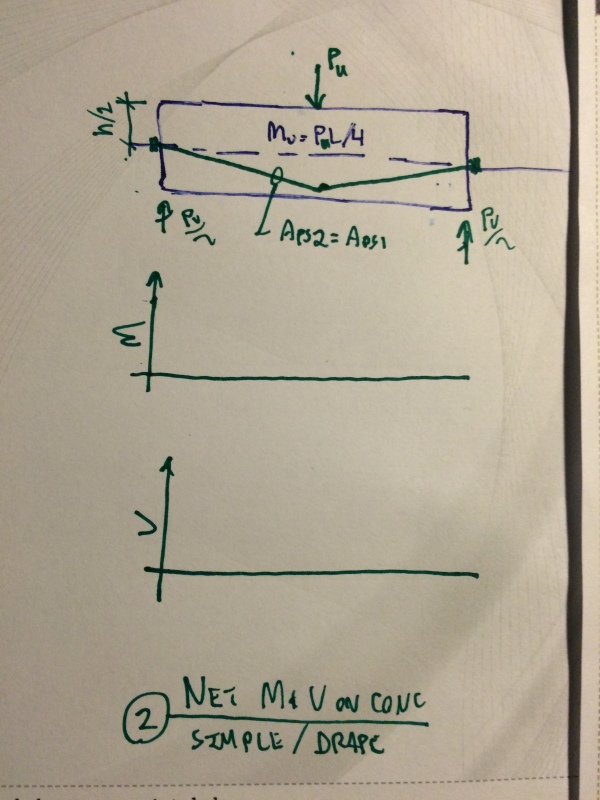
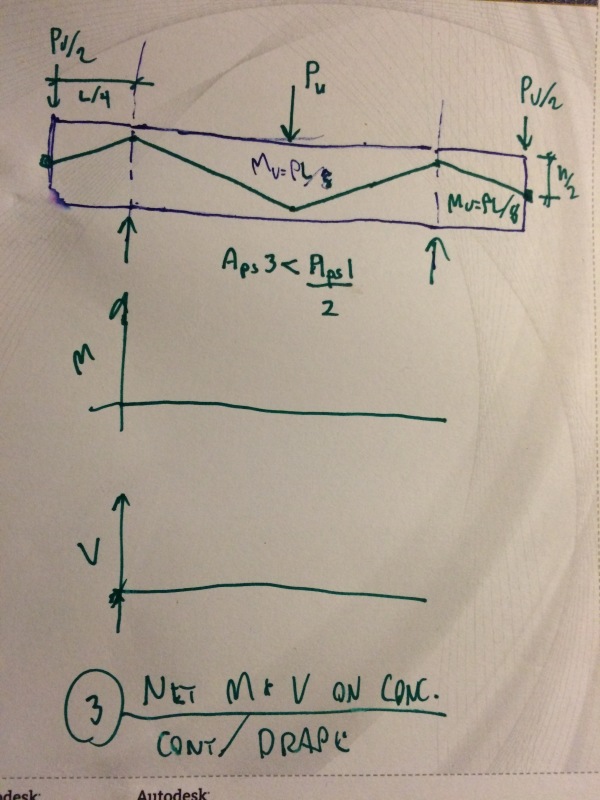
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
- Status
Similar threads
- Question
- Question
- Question
