RFreund
Structural
- Aug 14, 2010
- 1,885
I'd like to bring this question back up:
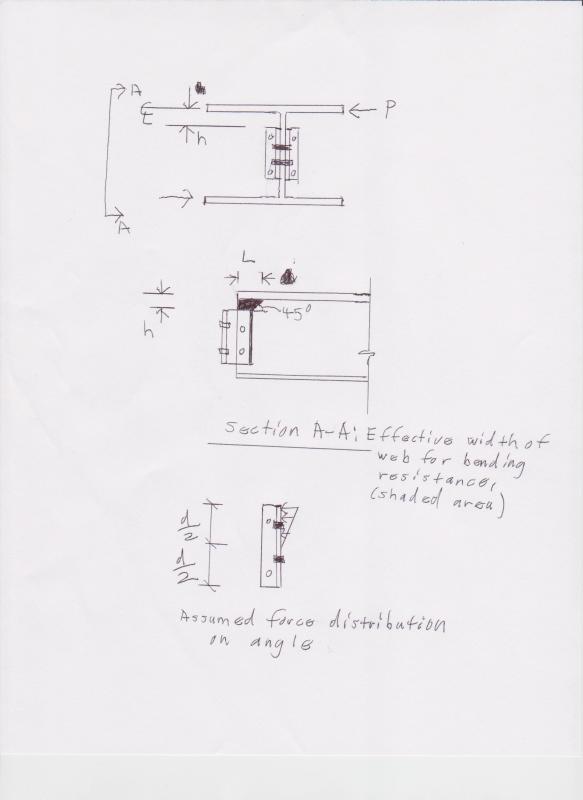
I'm trying to get a list of checks for this situation. Especially for the beam web and double angles.
For the beam web, can you simply add shear stress plus torsional shear stress?
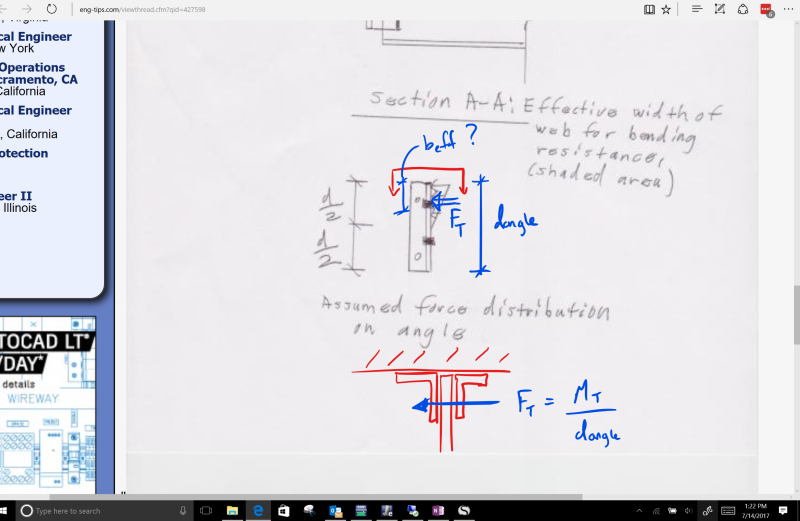
For the double angles - BA suggests a T/C couple and checking strong axis moment, but this sees odd to me as the angle is fastened to a support and you would probably get a significant amount of capacity. Checking the legs as tall thin rectangles in torsion seems pretty conservative. Breaking the torsion up into a T/C couple as M/(L.angle/2), then checking half the angle as "flange bending" seems like a possibility but also kinda odd.
Any thoughts?
Thanks in advance!
EIT
I'm trying to get a list of checks for this situation. Especially for the beam web and double angles.
For the beam web, can you simply add shear stress plus torsional shear stress?
For the double angles - BA suggests a T/C couple and checking strong axis moment, but this sees odd to me as the angle is fastened to a support and you would probably get a significant amount of capacity. Checking the legs as tall thin rectangles in torsion seems pretty conservative. Breaking the torsion up into a T/C couple as M/(L.angle/2), then checking half the angle as "flange bending" seems like a possibility but also kinda odd.
Any thoughts?
Thanks in advance!
EIT