sendithard
Industrial
Is the below valid without locking down rotation so you have a plane to measure distance from x and/or y distance from?
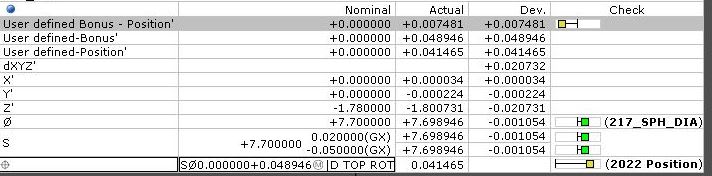
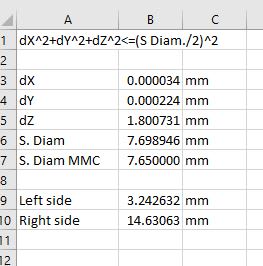
The datum cylinder A defines X & Y in location and datum plane B defines the true position distance of the sphere below said plane. So in theory you can garnish a radial deviation from this true position in space, but what you can't do is define said deviation from a X and Y plane. So you have your overall deviation, but it can't be quantified with the typical X & Y deviation. Therefore, I'm wondering if this particular callout is valid b/c the rotation isn't locked down via a tertiary datum ref frame.
Thanks.
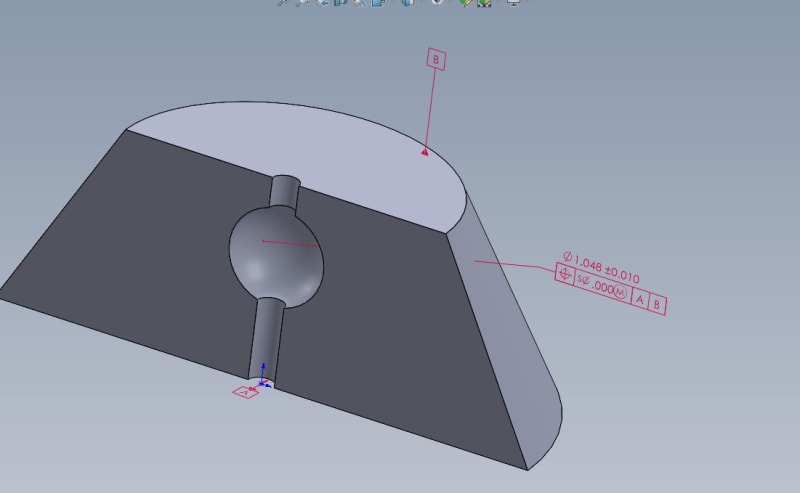
The datum cylinder A defines X & Y in location and datum plane B defines the true position distance of the sphere below said plane. So in theory you can garnish a radial deviation from this true position in space, but what you can't do is define said deviation from a X and Y plane. So you have your overall deviation, but it can't be quantified with the typical X & Y deviation. Therefore, I'm wondering if this particular callout is valid b/c the rotation isn't locked down via a tertiary datum ref frame.
Thanks.