Navigation
Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
More options
Style variation
-
Congratulations cowski on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
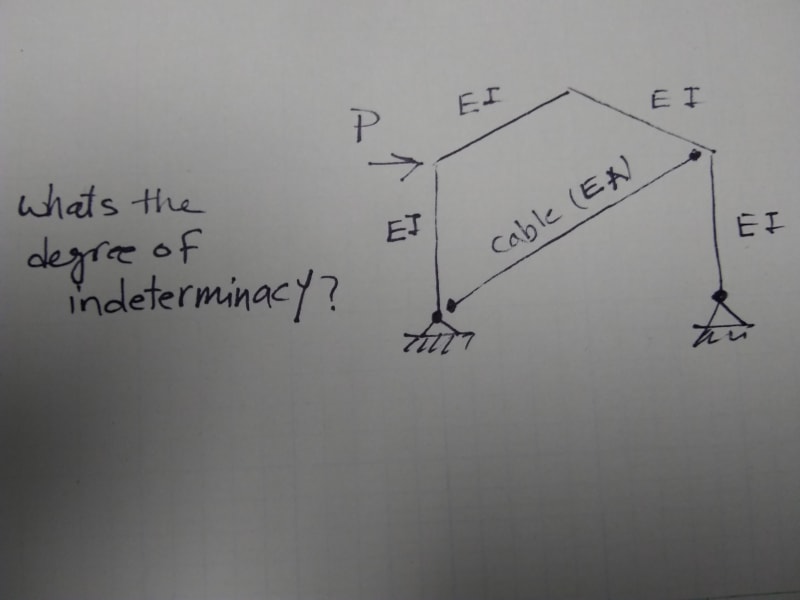
Degree of indeterminacy 4
- Thread starter SKJ25POL
- Start date
- Status
- Not open for further replies.
With or without the cable, the structure has one degree of indeterminacy unless second order effects are considered. It is not standard practice to consider a change in structural geometry due to member elongation (in this case cable elongation). If you did, then the degree of indeterminacy would be two.
Without the cable, it would be a three hinged arch if the peak joint is a pin.
With the cable, for a horizontal force from right to left, the cable is not engaged, so no change.
Changing the joint at top of right hand column to a pin, the sloping cable carries all of the horizontal force. The reactions are determinate. Vertical reactions are equal and opposite.
BA
Without the cable, it would be a three hinged arch if the peak joint is a pin.
With the cable, for a horizontal force from right to left, the cable is not engaged, so no change.
Changing the joint at top of right hand column to a pin, the sloping cable carries all of the horizontal force. The reactions are determinate. Vertical reactions are equal and opposite.
BA
BA said:Changing the joint at top of right hand column to a pin, the sloping cable carries all of the horizontal force
Some of the force is carried by bending of the rigid elements. You still can't solve the internal forces with statics.
Tomfh said:Some of the force is carried by bending of the rigid elements. You still can't solve the internal forces with statics.
You are mistaken, Tomfh. There is bending in rigid elements, but if column height is h and distance between supports is L, then V = P*h/L each column, compression on the right, tension on the left. The horizontal reaction at the left column is P, so all moments can be calculated from these forces.
BA
No moment distribution needed. Label the nodes A,B,C,D,E starting from bottom left and ending bottom right. With a pin at Node D, the cable force is known to be P(h2+L2)1/2/L. The cable prevents sidesway, so the moment at any point in Members BC and CD can be determined directly from the force at Node D. The force in the columns is purely axial.
BA
BA
Tomfh,
The structure is indeterminate, but only to the first degree. I suggested making it determinate by changing a rigid joint at D to a pin. That makes it a determinate structure which can be solved, but to solve the actual structure, you still have to apply equal and opposite end moment to members CD and DE at point D to in order to equalize the slopes.
The original question was what is the degree of indeterminancy. I say that, with or without the cable, the answer is one.
BA
The structure is indeterminate, but only to the first degree. I suggested making it determinate by changing a rigid joint at D to a pin. That makes it a determinate structure which can be solved, but to solve the actual structure, you still have to apply equal and opposite end moment to members CD and DE at point D to in order to equalize the slopes.
The original question was what is the degree of indeterminancy. I say that, with or without the cable, the answer is one.
BA
BA said:I suggested making it determinate by changing a rigid joint at D to a pin. That makes it a determinate structure which can be solved
How though? How do you calculate the internal forces in the bars and the cable without performing stiffness analysis? How do you do it with equations of statics?
It is really no different than taking a two hinged arch, which has one degree of indeterminacy, and making it a three hinged arch which is statically determinate, then solving for the moment required at the added hinge to equalize the member slopes. You do not solve the two hinged arch by using equations of statics, but by adding only one hinge, you have demonstrated the degree of indeterminacy of the system.
In the present problem, the addition of a cable has not changed the degree of indeterminacy, which is all I am attempting to show.
BA
In the present problem, the addition of a cable has not changed the degree of indeterminacy, which is all I am attempting to show.
BA
BA said:which is statically determinate
Ok then, add the hinge at node D, and calculate the forces using statics? How do you do it? What is the force in the cable and the bars?
if a roller at the RH then the frame is (at least) externally determinate; lateral reaction at the LH point, and an up/down vertical couple.
if pinned on the RH (as per original problem) then this creates a redundancy (with lateral load at both LH and RH supports).
if the upper LH joint is fixed then it (the LH vertical) can react some applied load, with most of the load going up the peak and down the cable.
then this creates another redundancy.
I`m in the "two" camp ... now.
another day in paradise, or is paradise one day closer ?
if pinned on the RH (as per original problem) then this creates a redundancy (with lateral load at both LH and RH supports).
if the upper LH joint is fixed then it (the LH vertical) can react some applied load, with most of the load going up the peak and down the cable.
then this creates another redundancy.
I`m in the "two" camp ... now.
another day in paradise, or is paradise one day closer ?
Tomfh,
I have already answered that question for the determinate structure. With a pin at Node D, the cable force is P(h2+L2)1/2/L; the axial force in columns AB and DE is P*h/L tension and compression respectively. The axial force in BC and CD is P/cosΦ where Φ is the slope of those members. The moment at point C is P*h' where h' is the rise from B to C or D to C.
To solve the indeterminate structure, a moment must be added at Node D to equalize member rotation at that point. I have not solved for that.
BA
I have already answered that question for the determinate structure. With a pin at Node D, the cable force is P(h2+L2)1/2/L; the axial force in columns AB and DE is P*h/L tension and compression respectively. The axial force in BC and CD is P/cosΦ where Φ is the slope of those members. The moment at point C is P*h' where h' is the rise from B to C or D to C.
To solve the indeterminate structure, a moment must be added at Node D to equalize member rotation at that point. I have not solved for that.
BA
BA said:With a pin at Node D, the cable force is P(h2+L2)1/2/L; the axial force in columns AB and DE is P*h/L tension and compression respectively.
The axial force in the left hand column is not simply the reaction at the left support, regardless of whether D is pinned. Some of the tension from the left support is resisted by the cable, and some by the column.
The force in the members depends upon their relative stiffnesses, not just equations of statics.
HTURKAK
Structural
- Jul 22, 2017
- 3,348
I screened the posts.. My respond could be repetition of one of the posts..
Degree of indeterminacy for Two-Dimensional Rigid-Jointed Frames is ;
Id= [(3m)+r]−3n - no. of releases
m= no. of members = 5
r= no. of support reactions = 4
n= no. of nodes = 5
no. of releases for this case = 2 , the moment releases for the cable element at both connections..
Id= 15+4-15-2=2
Degree of Indeterminacy is 2 ...
However, if the loading was in reverse direction ( the cable element will not take compression ) and if we neglect the own weight of the frame, Degree of Indeterminacy would be =1
I was wrong! I am sorry for unnecessarily prolonging the discussion.
Upon further consideration, I agree that the degree of indeterminacy is 2 when the cable is stressed in tension and 1 when it is removed or relaxes under load. Without the cable, the structure is a two hinged arch, so the cable is a redundant member.
BA
Upon further consideration, I agree that the degree of indeterminacy is 2 when the cable is stressed in tension and 1 when it is removed or relaxes under load. Without the cable, the structure is a two hinged arch, so the cable is a redundant member.
BA
@r13: Per your previous comments it's:
- One degree of external indeterminacy. This is the amount of additional information required to sort the support reactions.
- Two degrees of internal indeterminacy. This is the amount of additional information required to sort the member forces. Like Tomfh said, the trapezoid is one degree internally indeterminate on its own.
- One degree of external indeterminacy. This is the amount of additional information required to sort the support reactions.
- Two degrees of internal indeterminacy. This is the amount of additional information required to sort the member forces. Like Tomfh said, the trapezoid is one degree internally indeterminate on its own.
- Status
- Not open for further replies.
Similar threads
- Replies
- 11
- Views
- 2K
- Question
- Replies
- 7
- Views
- 3K
- Question
- Replies
- 3
- Views
- 2K
- Question
- Replies
- 0
- Views
- 3K
- Question
- Replies
- 0
- Views
- 260