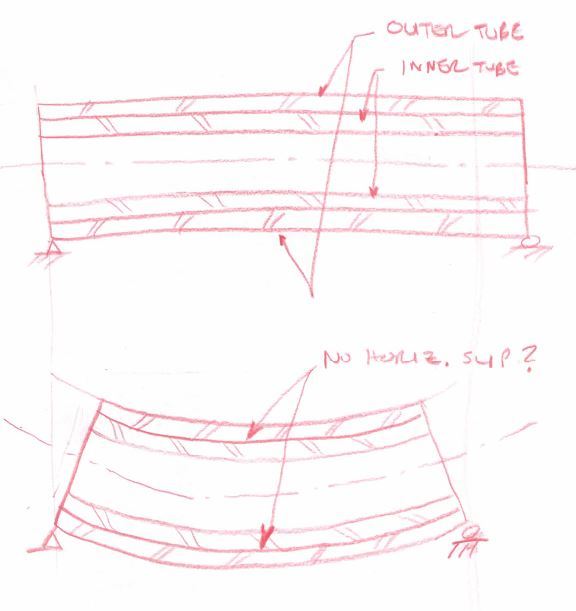
In this scenario, bonding is irrelevant. The neutral axes of both the inner tube and outer tube coincide in space and will share the same curvature. As such:
1) The two sections will behave compositely in flexure in the sense that matters: they will share a common strain diagram.
2) The composite section properties will be identical to the non-composite section properties (I_in + I_out).
So there you have it. You get composite behavior but, in this particular case, it's of no particular benefit.
OP said:
how is the section modulus for this configuration calculated?
Assume that the section behaves compositely (or non-compositely as it's irrelevant here) and calculate S = (I_in + I_out) / c
OP said:
I assumed, similar to composite beams, that two sliding tubes would be less stiff than one thick tube... Is this not true?
No, that assumption is incorrect in this instance.
OP said:
To clarify, I am trying to identify an effective single tube wall thickness to apply in an FEA model, to reduce complexity.
You can simply add the two tube wall thicknesses for equivalent flexural properties.
OP said:
Is it possible that the tubes would not tend to slide under bending, meaning there would be no difference if they were bonded?
That is indeed correct and is probably the key thing to understand about this situation.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.