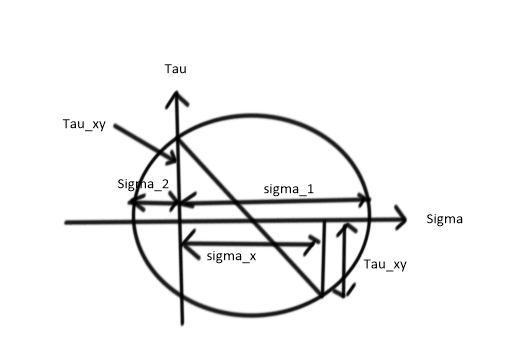
Hi All,
I need help calculating the combined stresses (max/critical stress) on the journal of a ball screw to determine FOS. I got the torsional stress and the axial stress (compression and tension), but I cannot remember how to combine them. I am trying to refresh on Mohr's circle from class over ten years ago, but admittedly it is throwing me for a loop. There is no bending stress or other shear stress, just pure axial and torsional, so it should be the same around the shaft circumference. Can anyone please help?
I need help calculating the combined stresses (max/critical stress) on the journal of a ball screw to determine FOS. I got the torsional stress and the axial stress (compression and tension), but I cannot remember how to combine them. I am trying to refresh on Mohr's circle from class over ten years ago, but admittedly it is throwing me for a loop. There is no bending stress or other shear stress, just pure axial and torsional, so it should be the same around the shaft circumference. Can anyone please help?