Beam on top of beam, not connected, and of different length. 7

[mecheng24]

http://www.eng-tips.com/viewthread.cfm?qid=110626

Hi all,

I was reading this thread, and one of the key points for the load to be shared was that beams must be spanning the same length. My question is, what if the top beam is only over the first 1/2 of the entire span. Does the load sharing still apply for the loads placed over that portion of the span?

Regards

 

[Archie264]

rb1957,

The scenario I considered had w on the upper beam and w on the portion of the lower beam without a beam above it. Upper beam extends to midspan. Therefore the loading on the lower beam is P = wL/4 at midspan and a uniform load of w on half the span. And "L" is the length of the lower beam.

 

[IDS]

I haven't been reading this thread because it didn't look particularly interesting from the first few posts. I got that wrong.

I hope I'm not too late to throw another spanner in the works.

With a stiff upper beam the load is transferred to the ends of the beam, and calculation of shears, moments and deflections is quite straightforward (making all the usual simplifying assumptions), but what happens as the stiffness of the upper beam is reduced, so that there is contact between the two beams along their length?

I have come to the conclusion that for a point load the upper beam will contact either at the two ends, or in the middle, but there will never be continuous contact. For a uniform distributed load there may be contact at the ends and in the middle, but there will still be no continuous contact.

My argument is as follows:
Consider two thin weightless beams, no shear deflections, plane sections remain plane, zero friction between the two beams (and anything else I may have forgotten).
For simplicity consider the short beam to be half the length of the long beam, placed symmetrically with a point load at mid span.

The upper beam is sufficiently flexible to contact the lower beam.

From symmetry both beams have zero slope at mid-span.

To remain in contact both beams must have the same curvature, so the bending moment at mid-span must be in proportion to their stiffness.

To remain in contact the slope and curvature must change at the same rate, so the bending moments must reduce in the same proportion, but the shear force is decreasing in the top beam and increasing in the bottom beam, so their bending moments cannot remain in the same proportion as we move along the beam.

It follows that the two beams can only be in contact at mid-span.

With a UDL the top beam may deflect to re-contact at its ends, but at this point it will have a different slope to the lower beam, and zero curvature, so this can only be a point contact.

Hence the upper beam may contact the lower at both ends, in the middle, or at all three points, but there can never be a continuous contact.

Of course in a real beam there is no such thing as a point load, the contact "point" will be distributed by non bending behaviour, and shear deflections will probably be significant, but even so I would expect the load transfer to be much more localised than a simple analysis might suggest.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[KootK]

It's an elegant argument IDS and I can't refute it in any rigorous manner. That being said, it just doesn't jive with my physical intuition. If I lay an unwelded 1/4" cover plate on top of a 30' long W21x44 and apply a significant uniform load, will there only be three points of contact? I'm skeptical.

I suspect that you're right that, strictly speaking, there is no continuous contact. However, I think it likely that there are more than three discrete points of contact. Depending on relative, stiffness, perhaps enough to approximate continuous contact.



I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[IDS]

KootK - I agree. So much so that I'm playing with the numbers in a spreadsheet right now, rather than doing the paid work I should be doing!

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[jfmann]

Doug.......commenting on the following from your post;

"To remain in contact both beams must have the same curvature, so the bending moment at mid-span must be in proportion to their stiffness.

To remain in contact the slope and curvature must change at the same rate, so the bending moments must reduce in the same proportion, but the shear force is decreasing in the top beam and increasing in the bottom beam, so their bending moments cannot remain in the same proportion as we move along the beam.

It follows that the two beams can only be in contact at mid-span."


Discussion to this point has varied between 2 different configuration of upper beam.........for now, per your stated conditions, we go back to configuration with upper beam centered within span of lower beam .....and with point load at midspan of upper beam.

First, there is no valid reason to limit conditions to "flexible" lower beam........one end of the spectrum is infinitely stiff lower beam and infinitely flexible (zero stiffness) upper "beam" (actually membrane)........for which case certainly upper beam simply takes shape of lower beam and there is complete continuous contact.

For conditions somewhere in middle of spectrum .....with both beams having stiffness between zero and infinite, but not necessarily equal .....and for condition when midspan of upper beam (supported at each end on lower beam) has deflection just enough to contact lower beam .........curvature of each beam is function of stiffness as well as loading..........both of which are different for each beam.

Note that initial instance of this condition occurs without any reaction force occurring at point of interior "contact"; picture upper beam just a micron above lower beam.

For upper beam to be in contact with lower beam only at midspan (of itself) ......but not at each end....is not possible since the following inconsistent conditions would have to exist at the same time;
1) Point load transferred directly through upper beam into lower beam.......such that there are no upward loads anywhere else against upper beam .....so that upper beam could only be straight, without any curvature.
(2) Lower beam would deflect due to point load and would therefore have curvature.........so that ends of straight upper beam would have to be in contact with lower beam.

More importantly, ....since slope of any beam is function of moment of inertia (I-value), length, load and position along beam.......it is clear that there are many combinations for two beams to have different slopes.

For example.......for configuration considered, slopes at x=L/4 (of main beam) are calculated using any method (conjugate beam, virtual work);

Upper beam, slope = PL^2/64EI-upper............which is standard PL^2/16 (for generic "L") for slope at end of beam, with L/2 input for actual length of upper beam
Lower beam, slope = PL^2/32EI-lower

So that, clearly.......slope of each beam is different, even for same I-value, which of course can vary from zero to infinite for each beam.

Bottom line.......in general, beams do not have same curvature


Indeterminate Behavior

To clarify previous post.......configuration is statically determinate when upper beam contacts lower beam at ends only.
When upper beam contacts lower beam at some interior point (between ends up upper beam), behavior changes to indeterminate.........meaning that equations of geometric compatibility must then be used to obtain solution for reaction forces at each point of contact. Interior support (provided by lower beam) for upper beam, between ends of upper beam, is then a spring-type support.........not a rigid (non-yielding) support.......since lower beam continues to deflect at that location.

As discussed in previous posts...........spreadsheet routine is very useful for such indeterminate conditions to illustrate behavior for range of beam stiffness and support configurations.



John F Mann, PE

http://www.structural101.com

 

[IDS]

For upper beam to be in contact with lower beam only at midspan (of itself) ......but not at each end....is not possible since the following inconsistent conditions would have to exist at the same time;
1) Point load transferred directly through upper beam into lower beam.......such that there are no upward loads anywhere else against upper beam .....so that upper beam could only be straight, without any curvature.
(2) Lower beam would deflect due to point load and would therefore have curvature.........so that ends of straight upper beam would have to be in contact with lower beam.

I agree with this point. To have any curvature there must be some shear transfer at points other than mid-span, so my suggestion of the point loaded beam contacting only at mid-span clearly does not work. There must be sufficient shear transfer at the ends of the short beam so that its curvature at mid-span is greater than that of the long beam. It will then have three points of contact, two ends and mid-span.

I will respond to the other points later; I have to go now.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[IDS]

jfmann - Responding to your other points:

Infinitely stiff lower beam and/or zero stiffness upper beam: Yes, in this case the two beams will remain in contact for any loading, and the upper beam will have no effect on the load distribution in the lower beam (assuming it is weightless). So my comments only apply to all real beams.

Curvature depends on stiffness as well as loading: Yes, but it remains true that for the two beams to be in contact over any finite length they must have the same slope and curvature over that length, so the ratio of bending moment to flexural stiffness must remain constant over that length.

..it is clear that there are many combinations for two beams to have different slopes: yes, in general the slope of the end of the upper beam will be different to the slope of the lower beam at that point. That is why they can't remain in contact. In fact they must have different slopes, because the curvature of the upper beam is zero, but the lower beam has a positive curvature, so if they had the same slope at the end point the upper beam would have to pass through the lower beam because it's downward slope was constant, whereas the lower beam was curving upwards.

Bottom line.......in general, beams do not have same curvature: That is the point. To remain in contact they must have the same curvature over the contact length, but due to the nature of the load transfer it is not possible for the curvatures to remain the same.


Regarding the behaviour of a beam with uniform load, I am now confident that this is the same as for a point loaded top beam; indeed the lower beam has no information about what the loading on the top beam is.

Starting with a comparatively rigid top beam, all the load will be applied as point loads at the top beam ends. If the stiffness of the top beam is now progressively reduced until the beams contact at mid-span, there will now be a load transfer a mid-span, as a point-load, and this behaviour will be the same no matter whether the load applied to the top beam is a uniform or a point load. The load at which contact occurs will be different, but the behaviour after contact will be similar, i.e. the contact point will remain a point.






Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[IDS]

Correction to the last point:

For a point load at mid-span there are always 3 point contacts, no matter how flexible the upper beam is (greater than zero), but for a UDL as the upper beam stiffness is reduced the contact will spread out from the centre, and the contact pressure will adjust so that the curvature of the two beams is equal over the contact length. At some point the contact pressure will reduce to zero, and the beams will separate until recontacting at the end of the shorter beam.


Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[jfmann]

Beams can be in contact without having the same curvature. Clearly this is seen at end of the upper beam.......as documented in my most recent previous post. However, this can only occur when slope of upper beam is less than (or equal to) slope of lower beam (allowing for point-contact)......which does result in new "twist", as discussed below.

Addressing following statement by Doug;
"In fact they must have different slopes, because the curvature of the upper beam is zero, but the lower beam has a positive curvature, so if they had the same slope at the end point the upper beam would have to pass through the lower beam because it's downward slope was constant, whereas the lower beam was curving upwards."


With load on upper beam, slope (curvature) at end of upper beam is not zero. Also, per my previous post, at end of upper beam, slope of each beam is different........for equal I-values, slope of upper beam is half the slope of lower beam for that specific configuration (upper beam centered on lower beam).

For future reference, I designate this configuration (upper beam centered on lower beam) as Case 2.
Per previous post....for Case 2....and based on assumption that contact at each end of upper beam is a point-contact (which is not correct for relatively low values of I-upper as discussed below).......contact first occurs when I-value of upper beam is (2/11) of the I-value of lower beam. Of course we are assuming constant I-value for each beam (and same modulus). We now calculate slope for each beam, at end of upper beam (x-lower = L/4). Actually, those are the same values as listed in most recent previous post since....for I-upper just less than (2/11) I-lower.....no force transfer occurs at this "contact" point. So now we just have to input the new I-upper;

Upper beam, slope = PL^2/64EI-upper = PL^2/[64E(2/11)I-lower] = 11PL^2/128EI-lower = 0.086 PL^2/EI-lower
Lower beam, slope = PL^2/32EI-lower = 0.031 PL^2/EI-lower

If correct, slope of upper beam would then be greater than slope of lower beam.....at end of upper beam. This can not occur.......such that there must then be some length of contact (instead of only point of contact) at end of upper beam. Such length of contact will change behavior (for both beams)......since assumed shape of upper beam will be different compared to only point-contact at end.

So now this becomes even more interesting;........Is end of upper beam "forced" to take on same curvature as lower beam for some length?.......If so, how does that alter behavior of each beam compared to assumption of only point of contact?

First thought is to assume, that yes, upper beam will then be forced to take on same curvature........and that this is "accomplished" by force transfer taking form of distributed load (whether constant-uniform or some other distribution) instead of point load at end of upper beam.

Of interest now is.......for what I-value does slope at end of upper beam first equal slope of lower beam?
This is easily answered by equating the two expressions above, so that (for Case 2).........I-upper = (1/2) I-lower

For lower value of I-upper, end of upper beam must then take on same curvature as lower beam. We must then calculate; (1) Location where slope of the 2 beams is no longer equal, and (2) Shape of distributed load at end of upper beam.........which I suspect (for now anyway) will be getting tad beyond "scope" of basic analysis since distributed load (at end of upper beam) must very likely be varying (non-constant)........and may even be non-linear. It may even be that gap occurs under end of upper beam, with contact occurring inboard of end of beam.








John F Mann, PE

http://www.structural101.com

 

[IDS]

Beams can be in contact without having the same curvature. Clearly this is seen at end of the upper beam.......as documented in my most recent previous post. However, this can only occur when slope of upper beam is less than (or equal to) slope of lower beam (allowing for point-contact)......which does result in new "twist", as discussed below.

Yes, they can be in point contact, but they cannot be in contact over any finite length unless both beams have the same slope at any section through the contact length. Therefore the curvature (rate of change of slope) must also be equal over the contact length, so the bending moments must be in proportion to the beam flexural stiffness values, as must the shear forces.

I have now satisfied myself that the way this works for an upper beam with a UDL is:
- There is a point contact at the ends of the beam.
- At mid-span they are in contact with zero shear and equal curvature.
- Moving away from mid-span they remain in contact with the UDL distributed such that the shear force and bending moments remain in the ratio of their flexural stiffness, hence the curvature of the two beams remains equal at any cross section.
- At some point the beams separate, such that the upper beam can have zero bending moment at the end, and the lower beam has a moment equal to the end reaction x the distance from the end of the upper beam to the support.
- At this point there is another point load transfer to maintain equilibrium.

I have modelled this behaviour in a spreadsheet, producing the graphs shown below. In the deflection graph (left) the red and blue lines show the beam deflections measured from the end supports (the blue line is hidden because the separation is very small). The green line shows the separation of the two beams (right hand scale), showing they are in contact for about 1 metre, then separate and re-join at the upper beam end. The bending moment diagram shows that the bending moments factored by the stiffness ratio (10) are exactly equal over the contact length, then diverge.

I have also uploaded the spreadsheet (see SSSpanU Example Tab), which uses the Excel Solver to find the end reaction, and uses a quadratic formula to find the contact length. But beware, it is very sensitive to changes in these two values, and needs a good starting guess, or it won't find a solution.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[jfmann]

Doug.......certainly "A" for effort........though your analysis is off

First.......lets clarify that configuration being analyzed is for upper beam (length L/2) centered within span of lower beam (length L).....and for uniform load on upper beam only.
For more general condition length of upper beam could be different (within limits so as not to result in drastically different configuration that would not be applicable) and loading on upper beam could be whatever you want.

Taking your conclusions in order;
(1) At end of upper beam......clearly, at lowest theoretical limit of stiffness for upper beam (I-upper = 0)......and with I-lower > 0.......upper beam is in full contact along entire length of upper beam. For positive, but very low value for I-upper, some gap eventually develops. However, without at least some mathematical basis, there is no basis for claim that contact at end of I-upper is limited to point contact. In fact, for uniform load on upper beam ...and for relative stiffness used for your analysis (I-upper = (1/10) I-lower) there must be some length of contact at each end of upper beam, as discussed below.

(2) For specific case you are considering, there is contact at midspan.........but this is not always the case, as discussed below, and as discussed at length in previous posts.

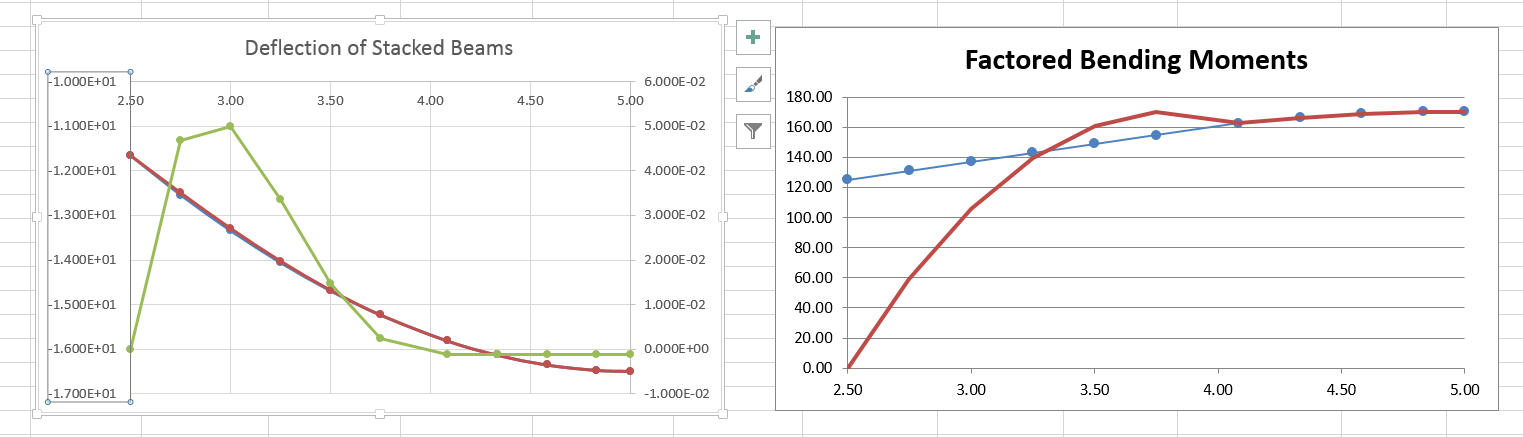
(3) This appears to be key flaw in your analysis. Moment (and shear) in each beam is not proportional to relative I-values (stiffness is not correct term since stiffness is function of E, I and L) wherever curvature is the same; see below for explanation. However, your moment graph already proves that this is not the case...........since, where red line crosses blue line, graph shows equal moments at point where the beams are not in contact and therefore do not have same curvature.

(4) Zero moment at end of upper beam is not caused (as implied by your statement) by separation of two beams somewhere between end and midspan of upper beam. Moment at end of upper beam is zero since that is always the case at end of beam that is free to rotate. Your description of moment in lower beam is correct only for x = L/4 (at end of upper beam). However, there is no obvious meaning to such statement.

(5) Meaning of "At this point" is not clear. More important is lack of free-body diagram to demonstrate "equilibrium" of upper beam.........which is most important flaw in your analysis.


Since your deflection graph lists absolute values.........you must be using specific moment of inertia values for each beam (which is fine for spreadsheet routine)........however such limited analysis is of course not useful for understanding general behavior for this setup.
Sounds like your analysis is for I-lower = 10 I-upper.........which is same as I-upper = (1/10) I-lower.
Red line in moment graphs must be for upper beam (with M = 0 at left end).
Explanation that solution is "very sensitive to starting value" is strong indicator that your analysis is not quite correct.

Based on your "timeline" of events, it sounds like you have started from an incorrect assumption that both beams start off with contact at midspan (only?)........and that the ends of upper beam mysteriously rise up above lower beam and then "reconnect" just as mysteriously at some future (unspecified) time.

If, as should be the case, analysis is for any moment of inertia values for upper beam (I-upper) and lower beam (I-lower)........then your claim that there must be contact at midspan of lower beam is not correct unless I-lower is infinite (in which case it is bedrock, not a beam!) or, more usefully, large enough.......relative to upper beam........such that deflection of upper beam results in such contact. Obviously, for a wide range of I-upper values (starting of course with theoretical "infinite"), deflection of upper beam (acting as simply-supported beam spanning between ends which are in contact with lower beam) is not enough to result in contact at midspan of each beam (for stated configuration).

For real-life demonstration of this behavior.......just review photos provided by SRE (above) which clearly show ......for point load and uniform load on upper beam.......continuous gap between both beams except at ends of upper beam.

As reported in previous posts........it is relatively straightforward to calculate value of I-upper that results in contact at midspan.........which is I-upper = (2/11) I-lower.
However, with I-upper = (2/11) I-lower, there is not yet any redistribution of load (compared to contact only at ends of upper beam) since upper beam has barely made contact (picture upper beam one micron above lower beam for I-upper infinitesimally less than (2/11) I-upper).

As value of I-upper is reduced below "first contact" limit (FCL; (2/11)I-lower ].......redistribution of load onto lower beam occurs, with lower beam providing an effective spring-type support for upper beam at midspan (of both beams). However, as discussed in my previous post, this is when behavior gets complex since contact at ends and midspan of upper beam is now over some length (instead of just point)......although, for at least some I-upper values near FCL, an assumption of point contact remains accurate enough for engineering purposes certainly and very likely for pure-analysis purposes as well.

As for relative slopes at end of upper beam (again, for stated case);

Slope of I-upper = wL^3/[192 E I-upper].........with "L" of course defined as L-lower.........and L-upper = L-lower /2 or L/2
Slope of I-lower = wL^3/[64 E I-lower].........obtained most conveniently via conjugate beam

Equating these two expressions results in.........I-upper = I-lower / 3
So that...........when I-upper is 33.3% of I-lower........slope (curvature) of each beam is equal at end of upper beam

Since this value of I-upper is greater than (as previously reported) value of I-upper that would result in first contact at midspan [ I-upper = (2/11) I-lower] if there were only point contact at each end......it is reasonable to conclude that slope of each beam is then the same at end of upper beam, before there is any contact at midspan.

As I-upper is reduced below (I-lower / 3)....but is greater than (2/11) I-lower (meaning no contact at midspan).......one of the following must be the condition at end of upper beam;

(1) Length of contact at each end must then be greater than zero
or
(2) Point of contact occurs inboard of end of upper beam........and there is no contact (gap) outboard of this new point of contact

For I-upper just less than I-lower / 3......slope of upper beam (at end) would have to be greater than slope of lower beam, except for the "obstruction" caused by contact with lower beam. The lower beam effectively causes an opposite rotation for end of upper beam............which is effectively the same as would occur if a moment is applied at end of upper beam causing opposite rotation. By calculating the difference in rotation for upper beam (that is, the "lost" rotation compared to condition without such obstruction), we can calculate amount of effective moment that has been applied by the upward force from lower beam.

Having now a modified expression for rotation of upper beam. If we know where to apply this moment (in opposite sense) to lower beam, we can then also determine modified expression for rotation of lower beam........which is necessary since force applied by upper beam is now distributed instead of point. We may then calculate modified slope of each beam along length of lower beam (which is of course the baseline).

Problem of course is determining where along lower beam this effective moment occurs (for lower beam)........or, stating another way, shape of distributed force along length of contact ...constant uniform, or uniformly varying or non-linear?

For relatively small length of contact......we might "reasonably" assume constant uniform distribution. However, as length of contact increases, shape of this distribution becomes critical for accurate analysis.

More development of necessary expressions is required for complete analytical solution........and makes me wonder whether anyone has bothered to do this before! (very likely yes, somewhere, sometime)
However, basic behavior is not as proposed by Doug above.

Finally.....claim that moment in each beam is proportional to relative I-values ......when beams have same slope (curvature)......is not correct. Moment graph by Doug shows that is not correct as previously noted. However, for more analytical demonstration........we can start by calculating moment in each beam at midspan, since (for this case) slope of each beam is of course the same value; zero.

M-upper = w(L/2)^2/8 = wL^2/32
M-lower = (wL/4)(L/2) - (wL/4)(L/4) = wL^2/8 - wL^2/16 = wL^2/16

So M-lower = 2 M-upper..........for all I-values for each beam...........that is, moment in each beam is not dependent on relative I-values

Also.......when slope at end of upper beam first equals slope of lower beam........moments are clearly not equal since M-upper = 0 and M-lower = (wL/4) (L/4) = wL^2/16









John F Mann, PE

http://www.structural101.com

 

[jfmann]

Just to clarify........for I-upper = (2/11) I-lower.......there would be contact (just barely) at midspan......only if contact at each end were point contact.

With distributed contact at each end of upper beam........what would otherwise be full rotation at end of upper beam is not allowed to occur (due to obstruction of lower beam being in the way)........resulting in some "effective moment" at end of upper beam that causes upward deflection of upper beam, relative to condition with only point contact at ends.

Therefore, since such distributed contact occurs for I-upper = (1/3) I-lower.....that is, for I-value greater than (2/11) I-lower....contact at midspan will not occur for I-upper = (2/11) I-lower.........there will still be some gap between beams at midspan.

At what value of I-upper this gap at midspan is finally closed is yet to be determined analytically (by myself anyway)........though, for now, I suspect there is some such value (which would of course have to be relatively low).

Also.......my conclusion (stated in previous post)........that contact at midspan occurs when I-upper = (1/10) I-lower, which is condition that Doug analyzed........may not in fact be correct since resistance to end-rotation of upper beam might even then be great enough (due to distributed contact at end of upper beam) to prevent such contact at midspan.

John F Mann, PE

http://www.structural101.com

 

[IFRs]

I actually read this entire thread and enjoyed it very much. I'm probably all wet but my contributions on this are:

1) the left end condition and the relative stiffnesses of the two beams are critical to understanding the solution.

2) if the left end of the top beam is on the support and the top beam is stiffer than the bottom beam such that there is essentially two-point contact between the two beams, fully half of the load on the top beam simply passes into the support and other than additional shear never makes it to the bottom beam. In this case, it does help the bottom beam if the bottom beam is not end-shear limited. Essentially, this can be generalized to say that the upper beam transfers some of the load towards the end of the lower beam, which is good for the lower beam until it becomes shear limited. So, in all cases as long as the upper beam carries some load to the end reaction it has to benefit the lower beam.

3) to the degree that either or both beams extend past or are short of the left support, the moment distribution in the bottom beam changes and so would it's deflection, stress, etc. Again, if any of the load is moved towards the end of the lower beam, it will help it.

4) if the upper beam is of great stiffness then it is a simple situation with two points of contact, with half the load now on the lower beam at the free end of the lower bean and no load sharing along the gap between the two beams.

5) if the upper beam is of minimal stiffness then it is again a simple situation this time with matching deflections along the beam interface.

6) when relative stiffness between the upper and lower beams is in somewhat comparable, the contact patches at the ends of the lower beam grow from zero (high upper beam stiffness) to some intermediate length of contact patch to perhaps fully in contact. This does not mean that the contact forces are equal, in fact I would expect them to vary. In these situations, the lower beam would feel a variable load distribution along some length at both ends of the lower beam. Again, if any of the load is moved towards the end of the lower beam, it will help it.

7) where there is load sharing along the entire length of the beam interface (non-uniform for any realistic stiffness of the upper beam), any additional load on only the lower beam causes additional lower beam deflection, a P-delta analysis will reveal where the next geometrical equilibrium exists and what the new extent of the contact areas are between the beams and how the contact forces vary within the contact patches. This new status changes the interaction between the two beams and must move the interaction along the continuum from uniform to two-point loads which in every case has to be worse for the lower beam.

8) a FEA analysis would clarify this easily

I'm probably full of sh.t but it was fun!

 

[IDS]

jfmann - I may respond in detail later, but we need to resolve the fundamental point of how two thin beams can be in contact over a finite length if their slopes are not equal over the entire contact length. If their slopes are equal then their curvatures must also be equal. You have not addressed this point.

Where they are not in contact the slopes and curvatures can be anything, but if the beams are in contact with different slopes and/or different curvatures then it can only be a point contact.

It follows that two beams of any finite stiffness can only be in contact over the full length of the shorter beam if the longer beam has zero moment at both ends of the upper beam (assuming transverse loading, and no friction between the beams), which is not the case for any of the examples discussed here.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[IFRs]

I would agree that two curves of different curvatures in theory have very limited contact but I disagree to the extent that they are elastic and therefore will deform and small deformations are all that is needed to increase the contact patch from a thin line to a more substantive rectangle ( or more complicated shape depending on the shape of the beams ). In reality, I think there will be surface contact patches at both ends of the upper beam.

 

[IDS]

IFRs - yes, as for any point load the stress at the point would be infinite, so can't exist in a real beam. But we are talking Bernoulli bending with point loads, zero depth beams, small deflections, and zero shear deflection, just as we normally do for any other beam analysis.

In fact if we are talking about steel beams of normal dimensions I think the variations from simple beam theory would be fairly small. The point contact at the ends would extend to over a small length, and there will be some shear deflection effects, but that's about it.

By the way, is anyone else getting the display area here extended beyond screen width, or is it just me? Makes reading very difficult.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[jfmann]

IFRs, generally valid points.......which appear to be valid for both cases considered to date......though specifically you are discussing original case (Case 1), with one end of upper beam at end of lower beam and other end of upper beam at midspan of lower beam.

(6) For all practical purposes (and even for analytical purposes) point-contact occurs at each end of upper beam unless I-value of upper beam is low enough such that slope at end of upper beam (calculated for condition of point contacts) is equal to slope of lower beam.........or would be greater than slope of lower beam if free-rotation of upper beam were not prevented from occurring by lower beam. For what I have designated "Case 2", which is upper beam centered on lower beam, "low enough" means that I-upper <= I-lower/3. See below for discussion of this issue for Case 1.

(7) For Case 1......point-contact at each end may not be worst case (especially for shear).........since, for distributed contact at outer end of upper beam, some load that would (for point contact) be transferred (by upper beam) directly to support is now applied to lower beam, even though this load is very near end of lower beam.

(8) Though Finite Element Analysis might be of some use at micro-level near supports.......especially if bearing stress were critical.......I doubt such method is going to be of any benefit for understanding of the problem or the solution!


For Case 1........comparing slope of each beam is complicated by difference in elevation between ends of upper beam........due to deflection of lower beam at midspan.......which causes undeflected line of upper beam to rotate slightly (about end at support) with respect to initial level position.

For uniform load on upper beam........before considering macro-rotation of upper beam, we have the same result as for Case 2; I-upper = (1/3) I-lower
Slope of upper beam = w(L/2)^3/(24E I-upper) = wL^3 / 192E I-upper
Slope of lower beam = (wL/4)(L^2)/16E I-lower = wL^3 / 64E I-lower........with Point Load, P(at midspan)= wL/4

Initial (undeflected) line of upper beam rotates through an angle, the tangent of which is equal to midspan deflection of lower beam divided by length of upper beam (L/2). At support, this angle must be added to slope of upper beam (calculated for initial level position) to obtain actual slope of upper beam.

Midspan deflection of lower beam = (wL/4)L^3/48E I-lower = wL^4 / 192E I-lower
Tangent of angle = [wL^4/192E I-lower] / (L/2) = wL^3/96E I-lower
In usual parlance of analysis.......we take tangent of small angles to be equal to the angle (which of course is in radians already), so that;

Slope of upper beam = wL^3 / 193E I-upper + wL^3 / 96E I-lower

Now setting expressions for slope of each beam equal, we obtain the following (perhaps surprising) result.......I-upper = I-lower
This means that distributed contact occurs at outer end of both beams when I-upper is equal to or less than I-lower.
This can be understood by considering that half the total load has been transferred off of lower beam by upper beam........but even moreso due to deflection of lower beam, which adds to outer-end rotation of upper beam........such that upper beam can have relatively large I-value (compared to Case 2).

However, at inner end of upper beam.........we must subtract macro-rotation of upper beam, and set expression for slope of upper beam equal to zero-slope of lower beam at midspan, resulting in the following; ......I-upper = I-lower/2
This means that distributed contact occurs at inner end of upper beam when I-upper is equal to or less than 50-percent of I-lower.

For Case 1........point-contact will occur at each end of upper beam as long as I-upper is at least half of I-lower.










John F Mann, PE

http://www.structural101.com

 

[jfmann]

Doug........yes, posting is acting strange, with window being extended

Anyway.....believe my analysis addresses all combinations of I-values for each beam
Essentially, for Case 2.....as I-upper is decreased below limiting value (I-lower / 3)........contact "starts" at each end ......and increases toward midspan as I-upper continues to decrease.
Analytically at least......contact along full length of I-upper only occurs for I-upper = 0.

Up next (if feasible without resorting to high-powered analysis program, which, again I do not believe will be necessary) is to work out shape of distributed pressure when finite-length contact occurs.

Expanding on that issue;
When upper beam is flexible enough such that lower beam prevents full rotation of upper beam at ends of upper beam......lower beam does this by exerting (redistributed) upward force on upper beam that effectively can be considered to have the same effect (on upper beam) as a concentrated moment applied to end of "free" upper beam. That is because what would otherwise have been rotation of upper beam at end........and deflection of upper beam at midspan.......are now reduced. Another (and perhaps more insightful) way to consider this effect is to see that effective "span" of upper beam has been reduced.

At same time, center-of-gravity of force applied to lower beam (at each end of upper beam) is now moved closer to midspan of upper beam. Total force at (near) each end remains the same.
For Case 2.......this condition then results in greater (even though relatively small) deflection and rotation of lower beam......so that we get cycle of movements that converge to solution.
For Case 1........effect is more complex since effect (on lower beam) at one end of upper beam is opposing effect at other end.

Analytically.......this might devolve into some horrendous higher-order equation.........well, hopefully not!
Numerical solution may then be order of the day.

John F Mann, PE

http://www.structural101.com

 

[IDS]

John - You still haven't addressed my basic question. If two beams have different curvatures at the point of contact, how can that contact extend for any finite length?

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[jfmann]

For Case 2.......to at least get handle on effects of reducing I-upper below value that first results in distributed contact at each end......we can "simply" calculate effective span length (for upper beam) that results in same rotation as lower beam, at the "current" point of contacts (which are L/2 apart).

We then find that effective span length is reduced quickly;

For example.........if we consider I-upper = I-lower / 4..........which is less than limiting value of I-upper / 3
Effective span for I upper becomes 0.908 of L/2.....0.908 is cube root of (3/32)........meaning that, at each end, center-of-gravity of "reaction" force is moved inward about 5-percent of original span for upper beam (which is L/2).
Of course, now we have to "recalibrate" by calculating "refined" slope of lower beam at this new location........and the beat goes on!

Clearly there is higher-order equation to be developed.



John F Mann, PE

http://www.structural101.com