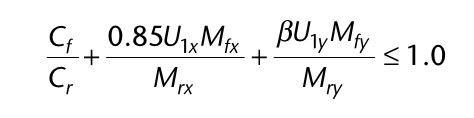KootK: You're making me bust out my old structural steel design text (Kulak & Grondin). Wouldn't be so bad but I am in the midst of a move and it was at the bottom of the tote! Why are engineering books so gosh darn heavy?
RE: Deformation
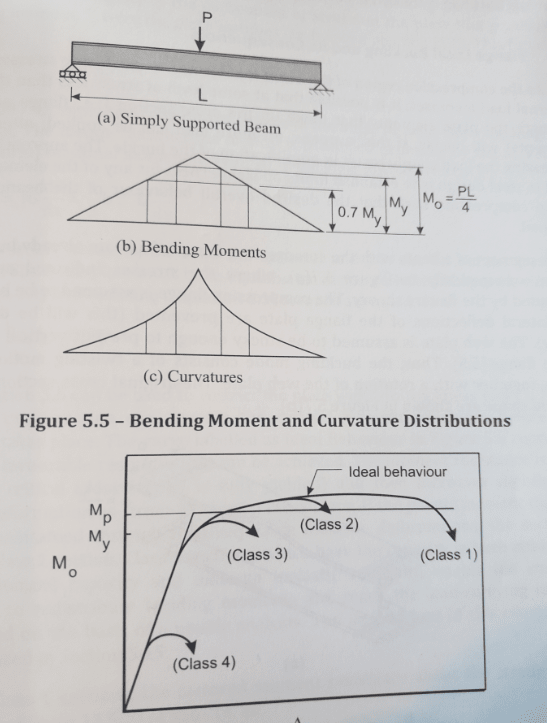
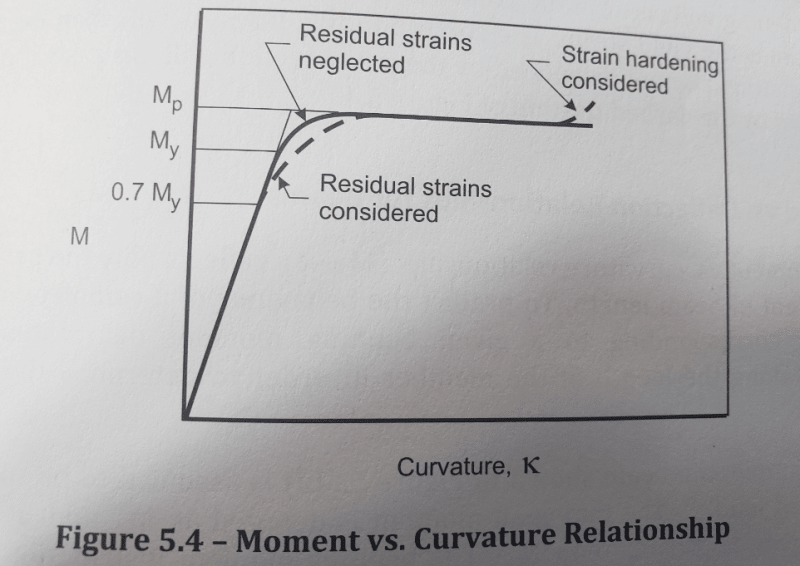
I think it's helpful to remember that even under so-called elastic loading (My), a beam would still be undergoing quazi-permanent deformation. In fact, deformation happens after only 70% of My. The thing is that
(A) it's really not a lot of deformation; and
(B) as
dik notes, the actual service loads never really getting to the design loads (My or Mp depending on the case) given material reduction factors and loading factors
This allows us to assume an elastic response to an My loading +/- unless there are large compressive residual stresses in the flange tips. And we do.
Now, for class 1/2 sections reaching Mp it's a bit harder to say that the deformation required to achieve Mp is negligible (as we did for My). But going back to what
dik mentioned, I think the small shape factor (Mp / My) combined with large loading factors keeps service loads much closer to My and hence things, generally speaking, don't become overly deformed even if designed to be (see above for My deformations being negligible).
Typical Shape Factor = 1.12 (W310x52) to 1.18 (W610x551)
Typical Loading Factors = 1.25 (Dead Loading) to 1.5 (Live or variable Loading)
Now, it isn't quite a 1:1 comparison because the loading factors take into account the statistical nature of load and the idealized nature of it in design (e.g. uniform when not really). But it does go to
dik's point that since the lowest typical loading factors is ~ 67% larger than the average Shape Factor (1.25 / 1.15) it seems reasonable to say that, on average, even if we design with Mp we are unlikely to get there in service.
RE: Beam-Column Design
I think it's the above that is keeping our beam columns from becoming unduly deformed in service rather than the U factor as you suggest. Lets take a look at a simple strong-axis bending + axial load case.
U1x = w / 1 - (Cf/Ce)
Well, w can be taken as 1.0 (13.8.5.b), and Ce is a function of member length. So we can arrange our example such that Cf = Cr << Ce by manipulating length of the member. And hence U1x = 1.0 (not punitive at all). For example, a W310x74 with K=1, Lu = 1250mm -> Cr = Cf = 2820kN << Ce = 206,972kN -> ~ U1x = 1.0
So our design equation reduces to,
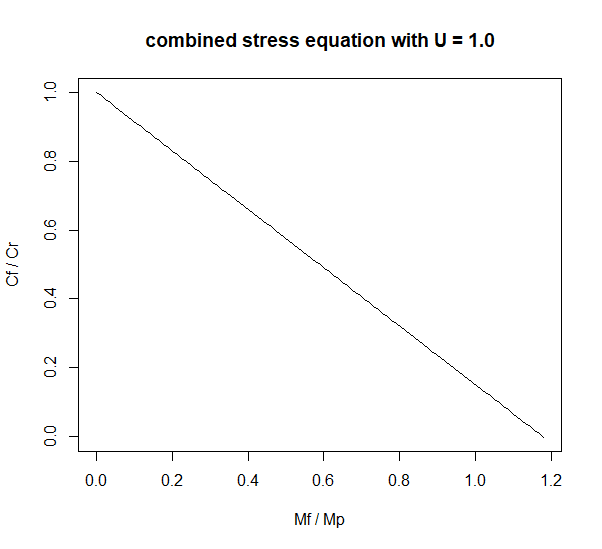
(Cf / Phi*A*Fy) + (0.85*Mf / Phi*Z*Fy) <= 1.0
The code as far as I can tell, never says a thing about transient loading states for a beam column. In other words, it is code compliant (maybe not a good idea but that's another thing) to have a beam that acts as a pure flexure member, pure axial member, and a combined member at various points in time during service as long as it (A) satisfies the individual equations when under pure loading and (B) satisfies the combined equation under combined loading. It should be noted that (0.85*Mf / Phi*Z*Fy) <= 1.0 in the combined equation will always be satisfied if Mf = Mr = Mp for a transient pure flexure state.
What I am getting at here, is if the beam-column was once used in pure flexure with Mr = Mp prior to being used as a beam-column at some later point (intentionally) then the code allows for this despite that beam perhaps having undergone permanent deformation! The code does not explicitly, nor by the U factor (as we saw above), necessarily take these deformations into account and that is likely to pose an issue under heavy(ish) axial loading as
KootK notes.
Realistically what is happening is service loads never get near actuals loads required to produce large, permanent deformation. And I think we have just been going along with it for so long, and that it has been satisfactory to this point, that really no change has been warranted.
IMHO I would probably keep Mr = My for a beam-column (especially one that has transient states) even if I could get more out of the code. Again, the savings are minimal (shape factor = 1.15) but possibility for bad things quite high. Not a good trade-off!