AISC Design Guide 1 - Appendix B

[Jerehmy]

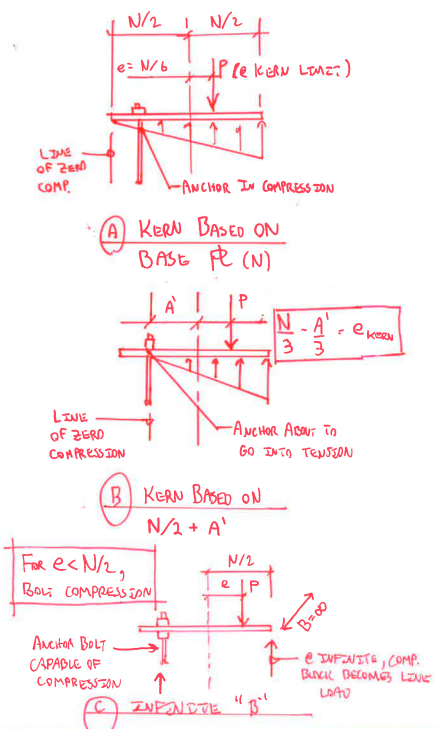
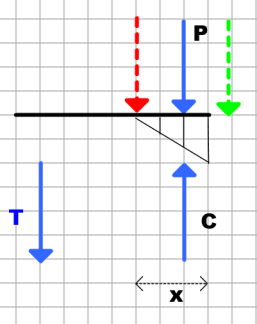
I have spreadsheets for both methods from AISC Design Guide 1 edition #2. I sent the triangular distribution method to a friend and he found an interesting situation where the anchor rod tension is negative even though e > e_kern. I for the life of me cannot figure out where the error is.

P_u = 110.55 kip
M_u = 47 kip-ft
B = 20 in
N = 16 in
N' = 14.5 in
A' = 6.5 in
f_pn = 2.224ksi (nominal concrete bearing capacity)

e = M_u/P_u = 5.102 in
e_kern = N/6 = 2.667 in

e > e_kern, thus large eccentricity moment

A = 0.5 * (3N` ± [ (3N`)² - 24(P_uA` + M_u)/(f_pnB) ]^0.5)

A = 0.5 * ((43.5 in ) ± [ (43.5 in)² - 24((110.55 kip)(6.5 in) + 47 kip-ft)/((2.224 ksi)(20in))]^0.5)

A = 39.072 in ; 4.428 in (4.428 in is obviously correct one)

T_u = f_pnAB/2 - P_u

f_pnAB/2 = (2.224 ksi)(4.428 in)(20 in)/2 = 99.5 kip

T_u = 98.5 kip - 110.6 kip = -12.1 kip


Can't figure out why. I thought it might be an error calculating A but I have triple checked it.

 

[BAretired]

I am unsure of the spirit of this comment, but I do not object to either design method.

There was certainly no offense intended. I was merely pointing out that the "new" method is an even further departure from your suggested way of solving the problem.

The original question was why is the anchor in compression, when e_kern says it should not be.

AISC has said it shouldn't and it seems you are saying that it shouldn't, but e-kern is not the critical value of e which determines whether or not the anchor rods are in tension or compression.

Consider a footing A by A with a load P at its kern point, i.e. A/6 from center. The bearing pressure will vary from 0 to 2P/A. Now, suppose P is placed at A/3 from center which is outside the kern point. The new position is still a kern point, but not of the whole footing. It is a kern point of only half of the footing; there is no pressure over half of the footing, then it varies from 0 to 4P/A. Provided 4P/A does not exceed permissible soil bearing pressure, that is considered acceptable to many engineers (although there are some who insist on staying within the kern of the whole footing).

I still believe my original conclusion is correct. Using the triangular design method noted (not the only the acceptable method) the bearing stress should be the applied bearing stress not the allowable bearing stress.

I don't dispute your claim if you insist upon using elastic design but I think AISC are looking at more of an ultimate strength criterion.

BA

 

[pete600]

haha okay I give up, but I would appreciate your feedback on a question I asked a few days ago titled, "ASCE 7-10 Extreme Weak Story Irregularity (5b)" I have not received a response

 

[BAretired]

Sorry Pete600, I am not familiar with the ASCE document and don't know what they are stating.

BA

 

[KootK]

Interesting discussion. I'm late to the party but I still believe that I have a little something to offer, even if it's just a summation.

1) As discussed above, the AISC procedure represents an ultimate capacity condition and assumes non-linearity and some degree of plastic behavior (the anchors if not the concrete). In comparison, the kern business is predicated upon a linear elastic stress distribution. The two procedures were never destined to jive. Shame on the design guide for suggesting otherwise.

2) As discussed above, "the problem is B". I've considered this hypothetically in detail C below where I've studied the case of a base plate with an infinite B dimension. In that scenario, the concrete compression block reduces to a line of resistance at the leading edge of the base plate. Clearly, for any eccentricity that would put the applied load over the base plate, the anchor bolt tension would be negative.

3) I believe that BA's sketch (below) does not represent the eccentricity at which we would first expect tension in the anchor bolts. Rather, his sketch represents the eccentricity at which no additional ultimate capacity could be gained without tension in the anchor bolts. There's an important difference there.

4) I think that the kern business actually would be a pretty good predictor of the eccentricity at which bolt tension would first manifest itself. See detail A below (classic presentation where the kern is based on the base plate perimeter). A modified version of the kern concept based on the anchor bolts (detail B below), would produce more accurate results still.

5) There must be a range of eccentricity somewhere between my detail B and BA's detail where the anchor bolts are in significant tension but the ultimate procedure would not indicate any design tension demand. That's a little disconcerting.

6) Of the misleading things built into the AISC design guide, the most misleading has not yet been discussed. The ultimate capacity procedure often implies anchor bolt strains in the post-yield range. And anyone who's dabbled with appendix D knows that an embedded anchor's ability to develop it's plastic capacity is anything but given in many cases.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[BAretired]

3) I believe that BA's sketch (below) does not represent the eccentricity at which we would first expect tension in the anchor bolts. Rather, his sketch represents the eccentricity at which no additional ultimate capacity could be gained without tension in the anchor bolts. There's an important difference there.

I agree with the above statement. Using an elastic analysis, tension will occur in the anchor bolts whenever strain exceeds zero. Using an ultimate strength approach, coupled with a triangular stress distribution proposed by the AISC Design Guide, anchor bolt tension is not needed until the eccentricity exceeds N/2 - x/3.

BA