Miran Fernando
Mechanical
Hello all,
I’m looking for some guidance on a calculation that I’m trying to do. I posted a similar recent thread titled 'Heating of air in enclosure - calculation and experiment discrepancy'. This question is in relation to the same device as the one in that other thread, but the enclosure is different and does not concern an experiment that I have done, at least not yet.
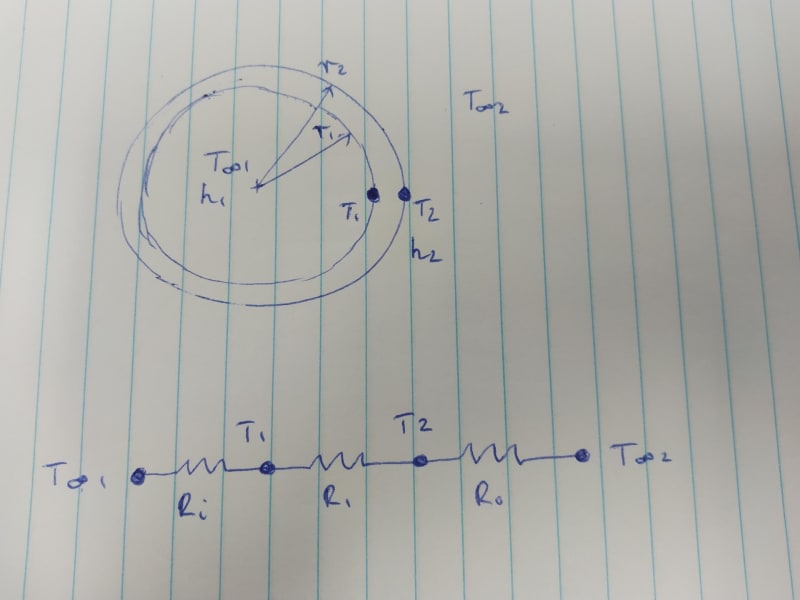
I have designed a small sealed cylindrical enclosure containing air and a small water-cooled device that needs to be kept cool in hot ambient conditions. I have a cooler that has around 75 W capacity to cool the device. The device’s peak power usage is around 60 W, as listed on the device datasheet and confirmed using a power meter (thanks to suggestion by IRStuff, EdStainless, and MintJulep in the other thread). The external ambient air temp is 40 °C. The enclosure is exposed to direct sunlight.
I would like to calculate what the air temperature is inside of the enclosure given:
Ambient air temperature is 40 °C,
Sunlight is incident on the enclosure,
Cooler liquid set point is 25 °C,
Some of the assumptions that I’m making are:
1. Half of the total surface area is exposed to solar irradiance 1000 W / m^2,
2. If the cooler liquid set point is 25 °C then the initial air temperature inside of the enclosure is also 25 °C,
3. All of the power dissipated by the device (60 W) is removed by the cooler, so any remaining capacity (75 – 60 = 15 W) is used to remove heat entering the enclosure from the outside environment,
My first thought on how to do this was to model it as a steady state problem and say that 'Energy in = Energy out' and rearrange to solve for the internal air temperature, but that conflicts with my second assumption (the assumption being that this is actually a transient problem and not steady state). I don’t think I’ve ever done a transient problem like this before. I calculated the Biot number to see if using lumped system analysis was appropriate, but I get a value much higher than 0.1 so it seems I should not use that method.
My second thought on how to do this was to create an expression saying 'Solar energy in = Convective energy out' to get to the internal air temperature when the system has reached steady state. I am again applying a steady state assumption, where the energy gained from solar irradiance equals the energy lost by convection of the enclosure to the surroundings. But I don't think that this takes into account the heat conducted through the walls of the enclosure into the internal air.
About the clearest thinking I have on this is that there is 15 W left of cooling power available. If the power entering the enclosure from outside is greater than 15 W, the air inside will begin heating up and the design needs to change.
I’m really not sure about how to proceed and would very much appreciate some guidance.
I’m looking for some guidance on a calculation that I’m trying to do. I posted a similar recent thread titled 'Heating of air in enclosure - calculation and experiment discrepancy'. This question is in relation to the same device as the one in that other thread, but the enclosure is different and does not concern an experiment that I have done, at least not yet.
I have designed a small sealed cylindrical enclosure containing air and a small water-cooled device that needs to be kept cool in hot ambient conditions. I have a cooler that has around 75 W capacity to cool the device. The device’s peak power usage is around 60 W, as listed on the device datasheet and confirmed using a power meter (thanks to suggestion by IRStuff, EdStainless, and MintJulep in the other thread). The external ambient air temp is 40 °C. The enclosure is exposed to direct sunlight.
I would like to calculate what the air temperature is inside of the enclosure given:
Ambient air temperature is 40 °C,
Sunlight is incident on the enclosure,
Cooler liquid set point is 25 °C,
Some of the assumptions that I’m making are:
1. Half of the total surface area is exposed to solar irradiance 1000 W / m^2,
2. If the cooler liquid set point is 25 °C then the initial air temperature inside of the enclosure is also 25 °C,
3. All of the power dissipated by the device (60 W) is removed by the cooler, so any remaining capacity (75 – 60 = 15 W) is used to remove heat entering the enclosure from the outside environment,
My first thought on how to do this was to model it as a steady state problem and say that 'Energy in = Energy out' and rearrange to solve for the internal air temperature, but that conflicts with my second assumption (the assumption being that this is actually a transient problem and not steady state). I don’t think I’ve ever done a transient problem like this before. I calculated the Biot number to see if using lumped system analysis was appropriate, but I get a value much higher than 0.1 so it seems I should not use that method.
My second thought on how to do this was to create an expression saying 'Solar energy in = Convective energy out' to get to the internal air temperature when the system has reached steady state. I am again applying a steady state assumption, where the energy gained from solar irradiance equals the energy lost by convection of the enclosure to the surroundings. But I don't think that this takes into account the heat conducted through the walls of the enclosure into the internal air.
About the clearest thinking I have on this is that there is 15 W left of cooling power available. If the power entering the enclosure from outside is greater than 15 W, the air inside will begin heating up and the design needs to change.
I’m really not sure about how to proceed and would very much appreciate some guidance.