Hi,
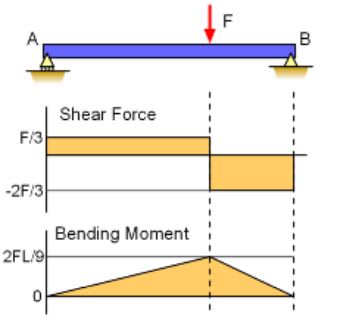
From the problem in the image, how do we express P in terms of F? Does the couple generated by the I-beam on top of simply supported beam translate as-is into the bottom section and we can draw this as just another beam with 3 point loads? I am trying to refresh my Strength of Materials knowledge but don't know how to approach this.
Thank you, in advance.
From the problem in the image, how do we express P in terms of F? Does the couple generated by the I-beam on top of simply supported beam translate as-is into the bottom section and we can draw this as just another beam with 3 point loads? I am trying to refresh my Strength of Materials knowledge but don't know how to approach this.
Thank you, in advance.


![[pipe] [pipe] [pipe]](/data/assets/smilies/pipe.gif)
![[2thumbsup] [2thumbsup] [2thumbsup]](/data/assets/smilies/2thumbsup.gif)