All,
I need to check if a table with a motor mounted on top of it will stand still or not under a rotational torque, i.e. starting torque of the motor.
I added a top view of the square table with 4 legs (black). The rotation axis of the motor is indicated with a blue dot and is not in the middle of the table.
The COG of the table with motor and other equipment is indicated with a yellow dot and is also not in the middle of the table, nor in the rotation axis of the motor.
How can I calculate the reaction forces of the 4 legs on the floor under the torque of 100 Nm? I need to check if the table will stand still or not as the legs cannot be bolted in the floor.
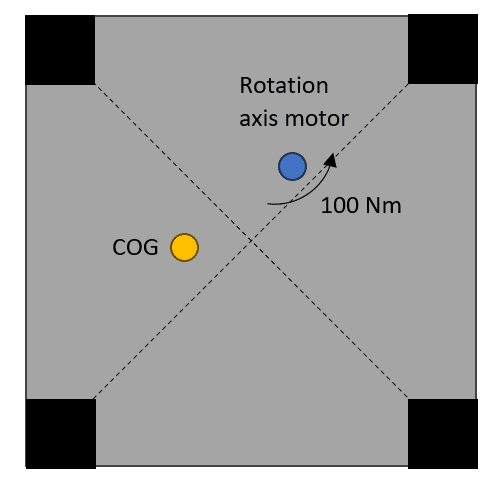
I need to check if a table with a motor mounted on top of it will stand still or not under a rotational torque, i.e. starting torque of the motor.
I added a top view of the square table with 4 legs (black). The rotation axis of the motor is indicated with a blue dot and is not in the middle of the table.
The COG of the table with motor and other equipment is indicated with a yellow dot and is also not in the middle of the table, nor in the rotation axis of the motor.
How can I calculate the reaction forces of the 4 legs on the floor under the torque of 100 Nm? I need to check if the table will stand still or not as the legs cannot be bolted in the floor.

