×
INTELLIGENT WORK FORUMS
FOR ENGINEERING PROFESSIONALS

Contact US

*
*
*
*

Thanks. We have received your request and will respond promptly.

Log In

Come Join Us!

Are you an
Engineering professional?
Join Eng-Tips Forums!
  • Talk With Other Members
  • Be Notified Of Responses
    To Your Posts
  • Keyword Search
  • One-Click Access To Your
    Favorite Forums
  • Automated Signatures
    On Your Posts
  • Best Of All, It's Free!
*Eng-Tips's functionality depends on members receiving e-mail. By joining you are opting in to receive e-mail.

Posting Guidelines

Promoting, selling, recruiting, coursework and thesis posting is forbidden.

Students Click Here

LU decomposition

thread552-506960

LU decomposition

LU decomposition

(OP)
Hi all,
I wonder why LU for this matrix retrieves such LU decomposition result.
M=
-0.5 -1 0
-1 -1 -1
0 -1 -0.5

L=
1 0 0
0 1 0
0.5 0.5 1

U=
-1 -1 -1
0 -1 -0.5
0 0 0.75



While it should be:

L=
1 0 0
2 1 0
0 -1 1

RE: LU decomposition

I suggest you use a screenshot, smiley emoticons don't help.

Here's some Octave

>> M=[.5,-1,0;-1,-1,-1;0,-1,0.5]
M =

0.5000 -1.0000 0
-1.0000 -1.0000 -1.0000
0 -1.0000 0.5000

>> [L,U]=lu(M)
L =

-0.5000 1.0000 0
1.0000 0 0
0 0.6667 1.0000

U =

-1.0000 -1.0000 -1.0000
0 -1.5000 -0.5000
0 0 0.8333

>> M=[-.5,-1,0;-1,-1,-1;0,-1,0.5]
M =

-0.5000 -1.0000 0
-1.0000 -1.0000 -1.0000
0 -1.0000 0.5000

>> [L,U]=lu(M)
L =

0.5000 0.5000 1.0000
1.0000 0 0
0 1.0000 0

U =

-1.0000 -1.0000 -1.0000
0 -1.0000 0.5000
0 0 0.2500

>> M=[1.5,-1,0;-1,-1,-1;0,-1,0.5]
M =

1.5000 -1.0000 0
-1.0000 -1.0000 -1.0000
0 -1.0000 0.5000

>> [L,U]=lu(M)
L =

1.0000 0 0
-0.6667 1.0000 0
0 0.6000 1.0000

U =

1.5000 -1.0000 0
0 -1.6667 -1.0000
0 0 1.1000

>>

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376: Eng-Tips.com Forum Policies http://eng-tips.com/market.cfm?

RE: LU decomposition

(OP)
Hi GregLocock,
thanks for your response. None of M matrix in your examples correspond to M in my example. Please try the M matrix in my example.

RE: LU decomposition

>> M=[-.5,-1,0;-1,-1,-1;0,-1,-0.5]
M =

-0.5000 -1.0000 0
-1.0000 -1.0000 -1.0000
0 -1.0000 -0.5000

>> [L,U]=lu(M)
L =

0.5000 0.5000 1.0000
1.0000 0 0
0 1.0000 0

U =

-1.0000 -1.0000 -1.0000
0 -1.0000 -0.5000
0 0 0.7500

Which is a very strange result, L is not triangular. Sorry I don't know enough about lu to explain what that means.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376: Eng-Tips.com Forum Policies http://eng-tips.com/market.cfm?

RE: LU decomposition

Using the Scipy.Linalg LU function via Excel:

If I set permute_I to false I get the same as hoshang:
Lower =
1 0 0
-0 1 0
0.5 0.5 1

Upper =
-1 -1 -1
0 -1 -0.5
0 0 0.75

If I set permute_I to true I get the same as greg:
Permuted Lower =
0.5 0.5 1
1 0 0
-0 1 0

Upper =
-1 -1 -1
0 -1 -0.5
0 0 0.75

So greg's results give the permuted lower matrix. I'd have to remind myself of how these things work to know what you do with that.

Where did the values:
L=
1 0 0
2 1 0
0 -1 1
come from?

Doug Jenkins
Interactive Design Services
http://newtonexcelbach.wordpress.com/

RE: LU decomposition

(OP)

Quote (IDS)

Where did the values:
L=
1 0 0
2 1 0
0 -1 1
come from?
Thanks. Review any textbooks on LU decomposition. You will find out that the decomposition would be

L=
1 0 0
2 1 0
0 -1 1

U=
-0.5 -1 0
0 1 -1
0 0 -1.5

RE: LU decomposition

OK, so Mathcad's LU decomposition is a general purpose decomposition, see https://www.cfm.brown.edu/people/dobrush/cs52/Math...

The function assumes that a permutation matrix P is required to make the decomposition work; this is why the lu() function returns 3 matrices.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! https://www.youtube.com/watch?v=BKorP55Aqvg
FAQ731-376: Eng-Tips.com Forum Policies forum1529: Translation Assistance for Engineers Entire Forum list http://www.eng-tips.com/forumlist.cfm

RE: LU decomposition

OK, so it seems the answer to the question:
I wonder why LU for this matrix retrieves such LU decomposition result.
is that there is more than one way to decompose a matrix.

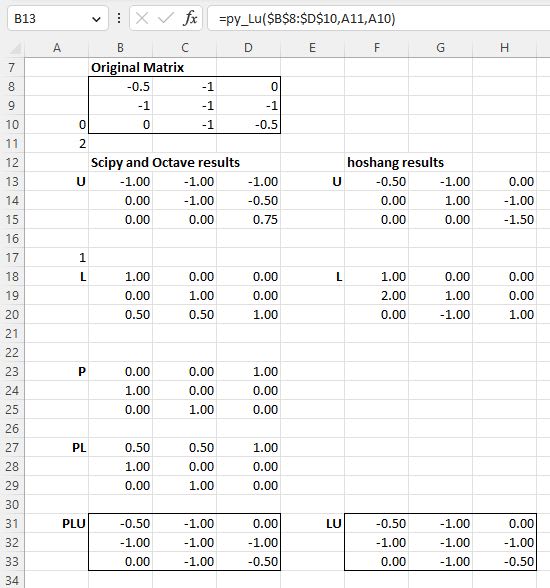
It seems that Scipy and Octave are using a pivotted lower matrix, so that for an original matrix A:
PLU = A
whereas for hoshang's matrices:
LU = A

Excel screen shot, calling Scipy fumctions:


Apparently Mathcad is doing something different, but I don't have Mathcad to see what is going on there.

Doug Jenkins
Interactive Design Services
http://newtonexcelbach.wordpress.com/

RE: LU decomposition

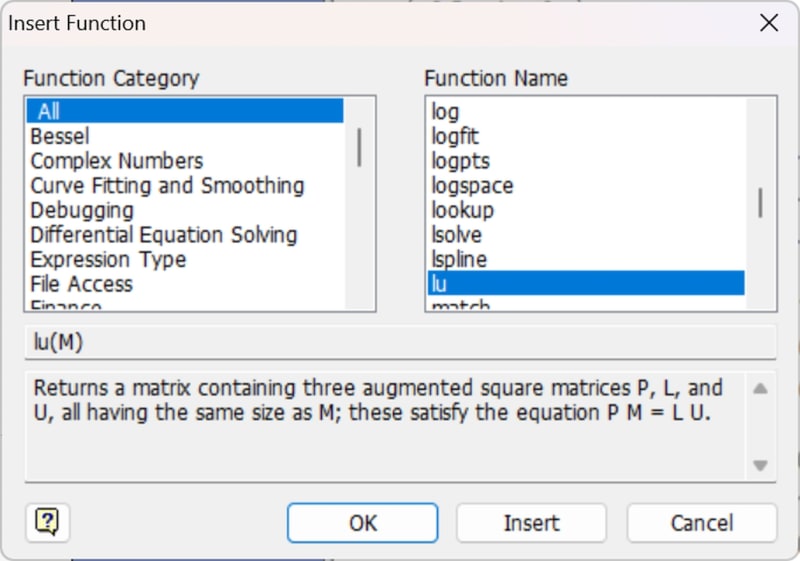
Mathcad is doing P*M = L*U, and the link I posted indicates that when LU decomposition is possible, there may be multiple solutions, and P in Mathcad's case is the inverse of the P in Doug's example, as can be seen below





TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! https://www.youtube.com/watch?v=BKorP55Aqvg
FAQ731-376: Eng-Tips.com Forum Policies forum1529: Translation Assistance for Engineers Entire Forum list http://www.eng-tips.com/forumlist.cfm

RE: LU decomposition

Thanks IRstuff

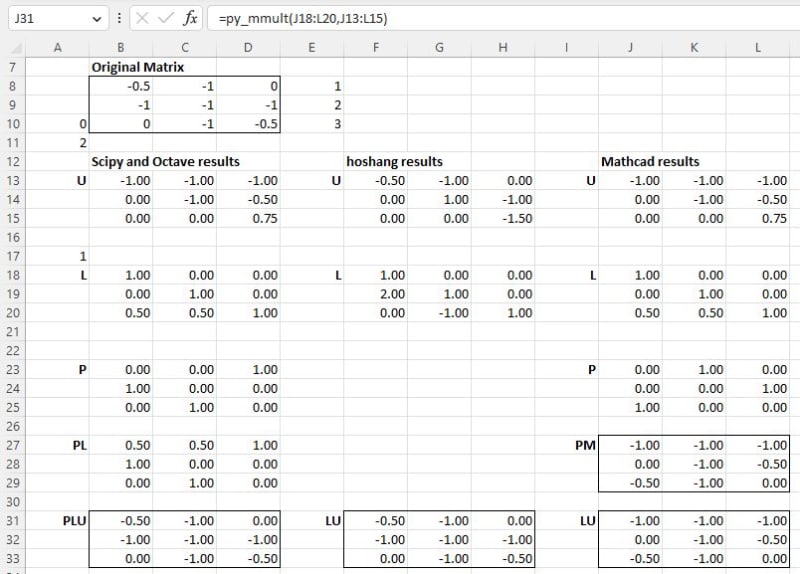
I have updated my spreadsheet to include the Mathcad way.

Doug Jenkins
Interactive Design Services
http://newtonexcelbach.wordpress.com/

RE: LU decomposition

(OP)
Hi all
So, how one can get hoshang results using Mathcad?

RE: LU decomposition

Quote (hoshang)

So, how one can get hoshang results using Mathcad?

I can't help with Mathcad, but why do you want to?

Doug Jenkins
Interactive Design Services
http://newtonexcelbach.wordpress.com/

RE: LU decomposition

This link has a good detailed description of the procedures for forming and solving LU matrices, with and without pivoting:
https://courses.physics.illinois.edu/cs357/sp2020/...#

It has python code for each stage of the process.

At the moment I'm having trouble getting their lu_decomp function to work. If anyone get's it working, please let me know.

.

Doug Jenkins
Interactive Design Services
http://newtonexcelbach.wordpress.com/

RE: LU decomposition

Quote (IDS)

At the moment I'm having trouble getting their lu_decomp function to work. If anyone get's it working, please let me know.

I have now got their code working. In the lu_decomp function:

Replace the two lines using np.block as below:

CODE --> python

# L = np.block([[L11, L12], [L21, L22]])
    # U = np.block([[U11, U12], [U21, U22]])
    L = np.zeros((n,n))
    U = np.zeros((n,n))
    L[0,0] = L11
    L[0,1:] = L12
    L[1:,0] = L21
    L[1:,1:] = L22

    U[0,0] = U11
    U[0,1:] = U12
    U[1:,0] = U21
    U[1:,1:] = U22

    return (L, U)

Also in the forward_sub function, replace:
for j in range(i-1):
with
for j in range(i):

With those changes the functions I tried seem to work correctly:
forward_sub
back_sub
lu_solve
lu_decomp

I haven't yet tried the functions using pivoting (but I'm working on it).

Doug Jenkins
Interactive Design Services
http://newtonexcelbach.wordpress.com/

RE: LU decomposition

(OP)
Hi,
What about my concerns?

RE: LU decomposition

Your original post has one questioned that has been answered in detail.

If you have remaining concerns perhaps you might tell us what they are.

Doug Jenkins
Interactive Design Services
http://newtonexcelbach.wordpress.com/

RE: LU decomposition

(OP)

Quote (IDS)

I can't help with Mathcad,

Quote (IDS)

Your original post has one questioned that has been answered in detail.

Quote (IRstuff)

You're just going to have to do your own LU decomposition.
My original post has one question that hasn't been answered.
Is there any workaround in Mathcad so that I can get hoshang results?

RE: LU decomposition

The question in the OP was:

Quote (hoshang)

I wonder why LU for this matrix retrieves such LU decomposition result.
to which the answer is:

Quote (IDS)

there is more than one way to decompose a matrix.

The link previously posted:
https://courses.physics.illinois.edu/cs357/sp2020/...
has a good clear explanation of how to do LU decomposition, with and without pivoting, and why it is a good idea to use pivoting for general use, to avoid problems if there are any zeros on the leading diagonal. It also has Python code which will generate the unpivoted matrices (after applying corrections as posted above).

You haven't told us why you have to use the unpivoted matrices, or why it has to be done in Mathcad, but if both are essential for some reason, and if Mathcad doesn't have that as an option, it shouldn't be too hard to convert the Python code to Mathcad, or you could look at using:
https://pypi.org/project/MathcadPy/
or something similar.

Doug Jenkins
Interactive Design Services
http://newtonexcelbach.wordpress.com/

RE: LU decomposition

Quote:

Full code to link the Scipy linear algebra functions, and the code above, to Excel via pyxll will be posted in the near future.


Thanks, do you know when you'll be posting the actual code?

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! https://www.youtube.com/watch?v=BKorP55Aqvg
FAQ731-376: Eng-Tips.com Forum Policies forum1529: Translation Assistance for Engineers Entire Forum list http://www.eng-tips.com/forumlist.cfm

RE: LU decomposition

IRstuff - it should be in the next few days. There will also be functions to call the Scipy linear algebra functions from Excel.

Doug Jenkins
Interactive Design Services
http://newtonexcelbach.wordpress.com/

RE: LU decomposition

Quote (PNatchwey)

There is python library for LU decomposition.

The great majority of the code in my link is for calling the Scipy linear algebra functions from Excel, including the LU decomposition functions.

The Python routines were written purely so I (and others) can see how the process works, in response to the question in the first post of this thread.

Also note that the download file includes links to the pyPardiso library which is very much faster than the Scipy LU functions.

Doug Jenkins
Interactive Design Services
http://newtonexcelbach.wordpress.com/

RE: LU decomposition

(OP)
Hi all
Any workaround using Mathcad.

RE: LU decomposition

As said on 22nd May:

You haven't told us why you have to use the unpivoted matrices, or why it has to be done in Mathcad, but if both are essential for some reason, and if Mathcad doesn't have that as an option, it shouldn't be too hard to convert the Python code to Mathcad, or you could look at using:
https://pypi.org/project/MathcadPy/
or something similar.

Doug Jenkins
Interactive Design Services
http://newtonexcelbach.wordpress.com/

Red Flag This Post

Please let us know here why this post is inappropriate. Reasons such as off-topic, duplicates, flames, illegal, vulgar, or students posting their homework.

Red Flag Submitted

Thank you for helping keep Eng-Tips Forums free from inappropriate posts.
The Eng-Tips staff will check this out and take appropriate action.

Reply To This Thread

Posting in the Eng-Tips forums is a member-only feature.

Click Here to join Eng-Tips and talk with other members! Already a Member? Login

Resources

Low-Volume Rapid Injection Molding With 3D Printed Molds
Learn methods and guidelines for using stereolithography (SLA) 3D printed molds in the injection molding process to lower costs and lead time. Discover how this hybrid manufacturing process enables on-demand mold fabrication to quickly produce small batches of thermoplastic parts. Download Now
Design for Additive Manufacturing (DfAM)
Examine how the principles of DfAM upend many of the long-standing rules around manufacturability - allowing engineers and designers to place a part’s function at the center of their design considerations. Download Now
Taking Control of Engineering Documents
This ebook covers tips for creating and managing workflows, security best practices and protection of intellectual property, Cloud vs. on-premise software solutions, CAD file management, compliance, and more. Download Now
Close Box

Join Eng-Tips® Today!

Join your peers on the Internet's largest technical engineering professional community.
It's easy to join and it's free.

Here's Why Members Love Eng-Tips Forums:

Register now while it's still free!

Already a member? Close this window and log in.

Join Us             Close