Tek-Tips is the largest IT community on the Internet today!
Members share and learn making Tek-Tips Forums the best source of peer-reviewed technical information on the Internet!
-
Congratulations TugboatEng on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
Dynamics Question
- Thread starter delast
- Start date
GregLocock
Automotive
Show us your working so far. We do not do your homework for you. It would probably be a good idea to tell us what you have recently studied in the course that set this problem, as there are several approaches. As a clue (i) is the hardest part in my opinion, and (iv) is trivial.
Cheers
Greg Locock
New here? Try reading these, they might help FAQ731-376
Cheers
Greg Locock
New here? Try reading these, they might help FAQ731-376
Seems to me that (iv) does require making an assumption about the vertical component.
TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! faq731-376 forum1529 Entire Forum list
TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! faq731-376 forum1529 Entire Forum list
GregLocock
Automotive
Yes, I'd guess no bouncing. It doesn't say but I'm assuming there is no tractive force either.
So, some intermediate questions
Do you need to know what is going on in the first arc?
What is the vehicle's velocity when theta = 60 degrees?
What needs to happen for the vehicle to take off? or if you prefer, remain in contact?
The reason I asked about what you were supposed to have learned that this is testing you on is that it is solvable with high school maths, but is an absolute bear to get a complete trajectory (which is more than the question asks for), I think. Whereas someone who is happy with integrating along a line or is studying lagrangians would do it quite differently.
Cheers
Greg Locock
New here? Try reading these, they might help FAQ731-376
So, some intermediate questions
Do you need to know what is going on in the first arc?
What is the vehicle's velocity when theta = 60 degrees?
What needs to happen for the vehicle to take off? or if you prefer, remain in contact?
The reason I asked about what you were supposed to have learned that this is testing you on is that it is solvable with high school maths, but is an absolute bear to get a complete trajectory (which is more than the question asks for), I think. Whereas someone who is happy with integrating along a line or is studying lagrangians would do it quite differently.
Cheers
Greg Locock
New here? Try reading these, they might help FAQ731-376
Yeah, I see the "Treat the car and driver as a particle" clause, so that kills the vertical component.
TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! faq731-376 forum1529 Entire Forum list
Compositepro
Chemical
The only change in total energy in the car is that lost in the shock absorbers. The ramp converts some of the horizontal kinetic energy to vertical velocity(energy), given by the angle at launch. This vertical energy is dissipated on landing. The horizontal energy (velocity) after landing is the same as at launch. There is also a small energy change due to the launch point being elevated above ground level.
- Thread starter
- #7
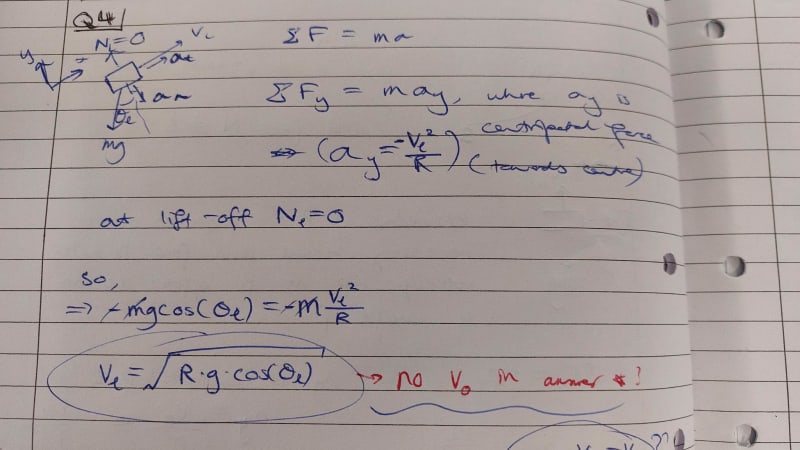
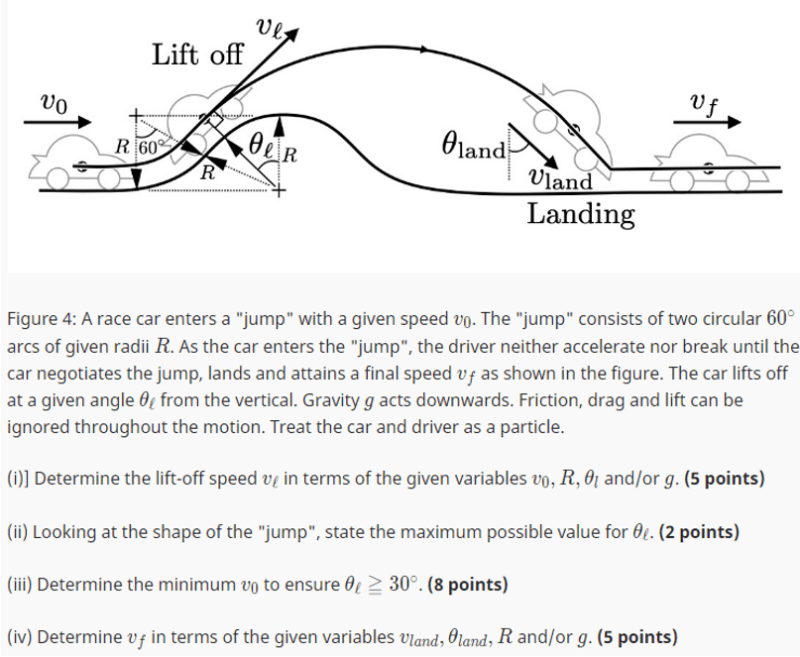
Hi, yes I've been having some difficult with the entire question as I'm unsure about question (i).
This is to do with systems of particle dynamics.
Here are two alternatives for my working. I'm not sure if they're on the right track. I know for sure that one of them is wrong as it doesn't include v0 in the final answer.
GregLocock
Automotive
@compositepro, I don't think horizontal (kinetic) energy is a helpful concept, at least for this question, and even in general. A vehicle's KE is 1/2.m.abs(v)^2, the x and z components can't be separated out in that equation. The landing trajectory as shown does not conserve energy.
Cheers
Greg Locock
New here? Try reading these, they might help FAQ731-376
Cheers
Greg Locock
New here? Try reading these, they might help FAQ731-376
GregLocock
Automotive
@delast, assuming no traction force, the speed at the intersection of the two arcs will be less than it was initially due to gain in PE (and so on and so forth as it climbs the second arc). You can try a force based approach for this bit, but it would involve solving an integral, energy methods are less hassle.
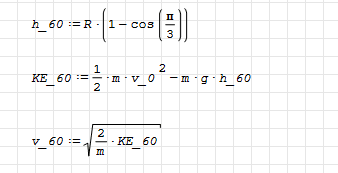
Cheers
Greg Locock
New here? Try reading these, they might help FAQ731-376
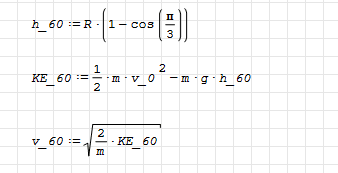
Cheers
Greg Locock
New here? Try reading these, they might help FAQ731-376
Compositepro
Chemical
Greg, you are correct. While energy is conserved, kinetic energy is not. However, momentum is conserved (this is what I had in mind). So, that is why the final horizontal velocity is equal to that at launch.
GregLocock
Automotive
@delast
your equation for v_L=sqrt(R*g*cos(theta_L)) is correct. v_0 isn't in there because it is the instantaneous situation that matters, not how you got there. Next step is to substitute in an equation linking v and theta and v_0
Also I think there's a typo in (iii), either they meant the maximum or the inequality is the wrong way round. Doesn't matter, just find v_0 for theta =30 degrees, you are right either way.
Cheers
Greg Locock
New here? Try reading these, they might help FAQ731-376
your equation for v_L=sqrt(R*g*cos(theta_L)) is correct. v_0 isn't in there because it is the instantaneous situation that matters, not how you got there. Next step is to substitute in an equation linking v and theta and v_0
Also I think there's a typo in (iii), either they meant the maximum or the inequality is the wrong way round. Doesn't matter, just find v_0 for theta =30 degrees, you are right either way.
Cheers
Greg Locock
New here? Try reading these, they might help FAQ731-376
- Status