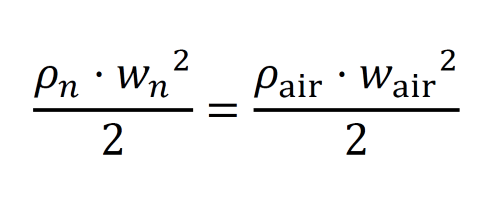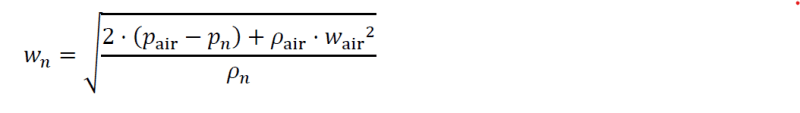Hi everyone,
I tried looking for something similar, but I have not found it.
I have measured the airflow (air speed) in the round ducting using a pitot tube and I need to find out the mass flow of it. At some point I must be making a mistake because when I calculate it from normal cubic meters per hour (Nm3/hr) I got a different value than when I calculate it from the actual flow (before converting to normal cubic meters).
Normal cubic meters are when gas is at:
tn= 0 deg Celsius (=273.15K)
pn = 1013,25 mbar.
densn 1.293 kg/m3 - density of air at normal conditions
d = 250mm - diameter of duct
A = 0.049m2(cross sectional area of the duct)
tair = 336°C (= 609K) - temperature of air in the duct
dair = 0.580 kg/m3 - density of air in the duct
pd = 0,825 mbar (= 82,5 Pa) - measured average dynamic pressure
w = 16,87 m/s - average air speed calculated from dynamic pressure ad velocity
Actual volumetric flow is:
f = w* A = 16,87 m/s * 0,049 m3= 0,828 m3/hr = 2981 m3/hr
To calculate the flow at normal conditions i first calculate the airspeed at these conditions. Assuming that in the duct the static pressure is equal to normal pressure
wn = w* sqrt (dair/dn) = 11,296 m/s
Flow at normal condition is
fn = wn* A = 0,55 Nm3/s = 1996 Nm3/hr
All of that seems easy but there must be an arror as when I calculate the mass from actual and normal flow I have different results
from actual flow
m = f * dair = 2981 * 0,580 = 1728 kg/h
from normalized flow
m = fn * dn = 1157 kg/h
The mass flow in kilograms should always be the same.
In the atatchment there is an excel file with the same calculations. I don't know where the dfference comes from. I calculated the compressibility factor (Z) for both states (actual and normal) but it is very close to 1, so that's not it. Can anybody direct me to the solution.
Regards,
Marcin
I tried looking for something similar, but I have not found it.
I have measured the airflow (air speed) in the round ducting using a pitot tube and I need to find out the mass flow of it. At some point I must be making a mistake because when I calculate it from normal cubic meters per hour (Nm3/hr) I got a different value than when I calculate it from the actual flow (before converting to normal cubic meters).
Normal cubic meters are when gas is at:
tn= 0 deg Celsius (=273.15K)
pn = 1013,25 mbar.
densn 1.293 kg/m3 - density of air at normal conditions
d = 250mm - diameter of duct
A = 0.049m2(cross sectional area of the duct)
tair = 336°C (= 609K) - temperature of air in the duct
dair = 0.580 kg/m3 - density of air in the duct
pd = 0,825 mbar (= 82,5 Pa) - measured average dynamic pressure
w = 16,87 m/s - average air speed calculated from dynamic pressure ad velocity
Actual volumetric flow is:
f = w* A = 16,87 m/s * 0,049 m3= 0,828 m3/hr = 2981 m3/hr
To calculate the flow at normal conditions i first calculate the airspeed at these conditions. Assuming that in the duct the static pressure is equal to normal pressure
wn = w* sqrt (dair/dn) = 11,296 m/s
Flow at normal condition is
fn = wn* A = 0,55 Nm3/s = 1996 Nm3/hr
All of that seems easy but there must be an arror as when I calculate the mass from actual and normal flow I have different results
from actual flow
m = f * dair = 2981 * 0,580 = 1728 kg/h
from normalized flow
m = fn * dn = 1157 kg/h
The mass flow in kilograms should always be the same.
In the atatchment there is an excel file with the same calculations. I don't know where the dfference comes from. I calculated the compressibility factor (Z) for both states (actual and normal) but it is very close to 1, so that's not it. Can anybody direct me to the solution.
Regards,
Marcin