VFreshEngineer,
I read your post on Friday and I have given it some thought. I have worked on stuff similar to this.
Caveat: I make a distinction between shock mounts, and anti-vibration mounts, and I watch my terminology. In design in general, fifty to ninety percent of solving your problem is understanding what the problem is.
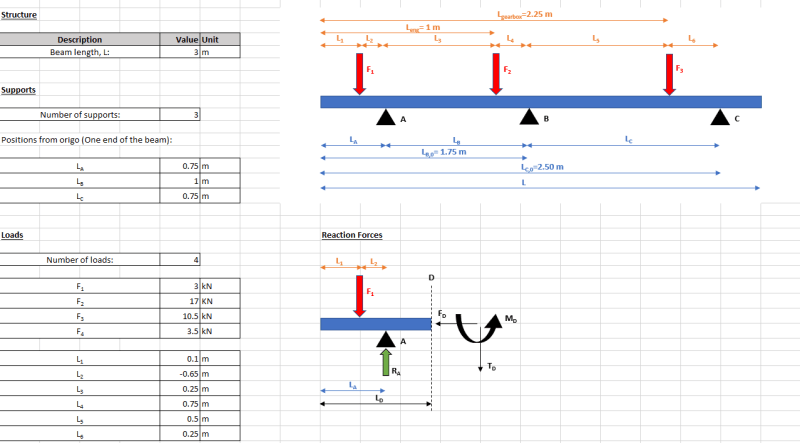
Your structure can be solved by double integration method if you assume it is flexible, and that it is sitting on an infinitely rigid base. This allows you to define boundary conditions that let you solve the statically interminate reactions.
In vibration analysis, your structure is infinitely rigid, and it is sitting on flexible mounts. Your optimal arrangement is for your mounts to be arranged symmetrically about your centre of mass. If your structure is set up symmetrically, each mount sees the same displacement and the same force. If your structure displaces a distance
x up or down, each mount will continue to exert equal forces. These will a function of
x, and your mounts' spring rate. If your structure rotates about the middle mounts, the fore and aft mounts will deflect in opposite directions, and the forces will vary correspondingly. Vibration is a dynamic condition. All kinds of weird things happen.
If your structure is not orders of magnitude more rigid than your anti-vibration mounts, then you have a weird and complex system.
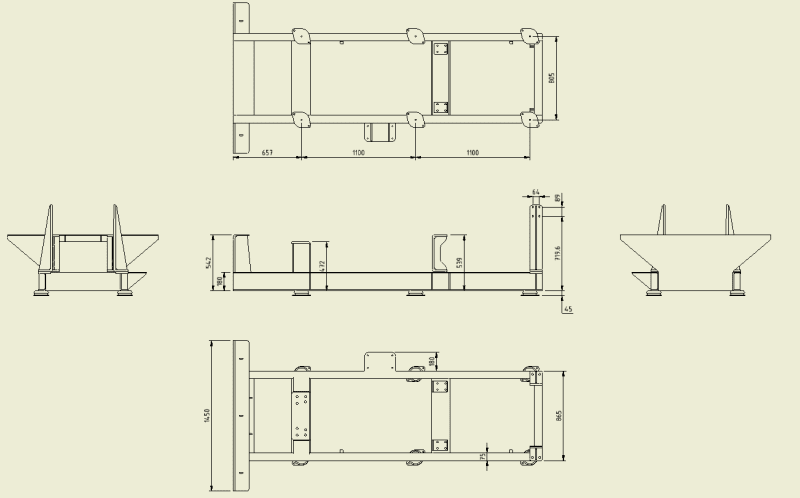
I have analysed a structure that sat on three sets of anti-vibration mounts. It was mounted inside an aircraft, so I had two problems.
[ol 1]
[li]The six mounts must be optimised for the mass of the device.[/li]
[li]The device must remain attached to the airframe in the event of an otherwise survivable crash.[/li]
[/ol]
Optimising was easy. All I had to do was look in the catalogue for mounts rated for one sixth the mass.
In a crash, the
cup[ ]style mounts should fail when they reach the end of their travel, and the top of the cup shears from the vertical load. In a forward crash, this will happen to the two rear mounts. The middle mounts will still exert spring load. The load ratings for aircraft style mounts like these account for crash safety, but I assume that they are assuming you are using four mounts. In the potentially deadly crash, the rear mounts will tear out before the middle mounts see their maximum load. Then, the middle mounts would max out and see the impact load. I don't really understand how this failure works. I am not sure I can just assume that the middle mounts are that much more strain energy to be dissipated. I was not the designer, so I could not change the mount arrangement. I think I bumped the mounts up a load rating, making the vibration setup less than optimal. I was not a happy camper.
If you have crash safety issues, I recommend four anti-vibration mounts, appropriately sized.
--
JHG