All,
I’m working on a simple beam plastic collapse static analysis for some basic benchmarking in Ansys WB. The problem in question is a solid rod (φ = 0.85”, 16” long, σy = 60 ksi) fixed at both ends. A concentrated load acts at the center of the rod at is applied till solver divergence. A mesh size of 0.1” is sufficient for mesh convergence.
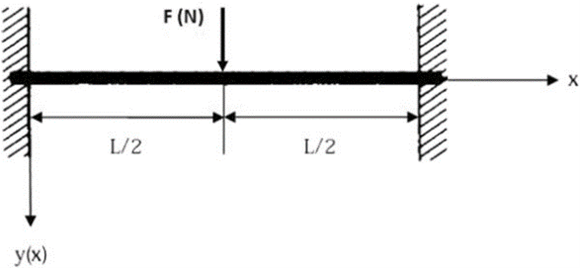
Hand Calcs: Wcollapse = 3070 lbf
a) Beam model, Elastic-Perfectly Plastic Material: Wcollapse = 3039 lbf
b) Beam model, Elastic-Plastic Material: Wcollapse = 3125 lbf (At the onset of instability and first bisection, but the solution converges to the applied 5000 lbf load)
c) Brick model, Elastic-Perfectly Plastic Material: Wcollapse = 3230 lbf
d) Brick model, Elastic-Plastic Material: Wcollapse = 3421 lbf (At the onset of instability and first bisection, but the solution converges to the applied 5000 lbf load)
NL Material:
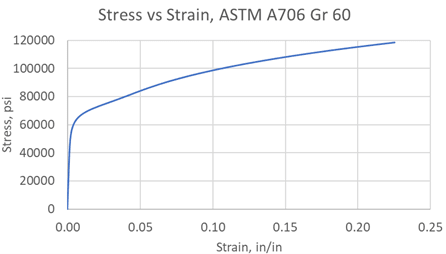
Q: Why does the solution continue bisection and converge while using an elastic plastic model? Is there a method to control this feature? The only warning in the log file at the first bisection is “The preconditioned conjugate gradient solver failed to converge, and therefore no solution was obtained. The equation solver is now being automatically switched to the sparse solver (EQSLV,SPARSE) to allow this analysis to continue". I do not get errors for excessive element deformation or large plastic strain increments typically associated with plastic collapse FEA.
Thank you
I’m working on a simple beam plastic collapse static analysis for some basic benchmarking in Ansys WB. The problem in question is a solid rod (φ = 0.85”, 16” long, σy = 60 ksi) fixed at both ends. A concentrated load acts at the center of the rod at is applied till solver divergence. A mesh size of 0.1” is sufficient for mesh convergence.

Hand Calcs: Wcollapse = 3070 lbf
a) Beam model, Elastic-Perfectly Plastic Material: Wcollapse = 3039 lbf
b) Beam model, Elastic-Plastic Material: Wcollapse = 3125 lbf (At the onset of instability and first bisection, but the solution converges to the applied 5000 lbf load)
c) Brick model, Elastic-Perfectly Plastic Material: Wcollapse = 3230 lbf
d) Brick model, Elastic-Plastic Material: Wcollapse = 3421 lbf (At the onset of instability and first bisection, but the solution converges to the applied 5000 lbf load)
NL Material:

Q: Why does the solution continue bisection and converge while using an elastic plastic model? Is there a method to control this feature? The only warning in the log file at the first bisection is “The preconditioned conjugate gradient solver failed to converge, and therefore no solution was obtained. The equation solver is now being automatically switched to the sparse solver (EQSLV,SPARSE) to allow this analysis to continue". I do not get errors for excessive element deformation or large plastic strain increments typically associated with plastic collapse FEA.
Thank you
