A few articles have been published recommending the use of a scaled load (action) effects to determine ultimate shear capacity for use with load rating to AS 5100.7. It is not clear from these articles why it is necessary to do that. Doing so will result in the strengths being different for design and load rating of a new bridge for a same vehicle (i.e. design vehicle is the same as nominated rating vehicle). Any input to this will be much appreciated.
Navigation
Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
More options
Style variation
-
Congratulations cowski on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Recommendation to scale factored action effects to determine shear capacity for load rating 1
- Thread starter kww2008
- Start date
- Status
- Not open for further replies.
- Thread starter
- #2
Can you provide some links?
At the moment I'm not sure what is being suggested.
Doug Jenkins
Interactive Design Services
At the moment I'm not sure what is being suggested.
Doug Jenkins
Interactive Design Services
- Thread starter
- #4
Hello Doug. The link of the published AJSE article is provided below. The article recommended that this approach be included in AS 5100.7 for shear load rating. The other papers publications referred to this article.
Settingsun
Structural
I've only given it a very quick skim, but is it just the effect that load rating means the stresses appears on both the load and capacity sides of the equation and vary until the loop is closed? I posted something to that effect in the thread linked below. The image (consisting of text) is what I'm referring to.
Basically, increasing the bending moment and shear force, like is done in load rating, reduces the shear capacity in MCFT. Load rating requires iteration in the new code whereas the old shear method just required one-step comparison between nominal shear force and known shear capacity.

Basically, increasing the bending moment and shear force, like is done in load rating, reduces the shear capacity in MCFT. Load rating requires iteration in the new code whereas the old shear method just required one-step comparison between nominal shear force and known shear capacity.

Settingsun
Structural
As a separate comment, I have seen load ratings be different from design. The first I came across MCFT, Qld Main Roads was using it to get more out of old pretensioned bridges that didn't have shear reinforcement. This was back when the code was still using the old calculation method.
- Thread starter
- #7
Hello stevenh49,
Response to the first comment.
The general equation for load rating can be shown as
RF = (phiV_u - V*_PL) / V*_LL
V_u = function of (V*,M*,T*) for example
MCFT requires consistency between the shear capacity and the applied load.
For a moving vehicle moving along a bridge, the combination of V*,M* and T* can be calculated for the bridge vehicle system at a key section for each incremental movement, say 0.1m for example.
The vehicle is moved along the bridge and the values of (phiV_u, M*, T*,V*) are calculated for all the steps. The RF of sections are calculated for every step and the smallest is chosen to be the RF of the bridge.
In accordance with the MCFT, the capacity used is consistent with the applied loading. No iteration is required.
The recommended approach in the article uses a set of factored load M*,V*,T* of the vehicle and the bridge system with the vehicle located to give the worse effects. A set of coefficients are calculated as:
eta_M = M*/V*, eta_T = T*/V*, and V is increased progressively starting from 0. M and T are calculated as M=eta_M V, T=eta_T V, and V_u is calculated from M,V and T. The iteration is continued until V=V_u. The V_u thus determined is not the V_u determined using direct calculation (which is the current practice). Interpreting in accordance with MCFT, the approach resulted in a V_u (proposed) that is for a scaled loading where the entire loading (both PL and LL) is scaled by a factor V_u(proposed)/V*. This capacity is not consistent with applied loading of the bridge vehicle system.
Response to the first comment.
The general equation for load rating can be shown as
RF = (phiV_u - V*_PL) / V*_LL
V_u = function of (V*,M*,T*) for example
MCFT requires consistency between the shear capacity and the applied load.
For a moving vehicle moving along a bridge, the combination of V*,M* and T* can be calculated for the bridge vehicle system at a key section for each incremental movement, say 0.1m for example.
The vehicle is moved along the bridge and the values of (phiV_u, M*, T*,V*) are calculated for all the steps. The RF of sections are calculated for every step and the smallest is chosen to be the RF of the bridge.
In accordance with the MCFT, the capacity used is consistent with the applied loading. No iteration is required.
The recommended approach in the article uses a set of factored load M*,V*,T* of the vehicle and the bridge system with the vehicle located to give the worse effects. A set of coefficients are calculated as:
eta_M = M*/V*, eta_T = T*/V*, and V is increased progressively starting from 0. M and T are calculated as M=eta_M V, T=eta_T V, and V_u is calculated from M,V and T. The iteration is continued until V=V_u. The V_u thus determined is not the V_u determined using direct calculation (which is the current practice). Interpreting in accordance with MCFT, the approach resulted in a V_u (proposed) that is for a scaled loading where the entire loading (both PL and LL) is scaled by a factor V_u(proposed)/V*. This capacity is not consistent with applied loading of the bridge vehicle system.
Settingsun
Structural
The idea of load rating is to determine how much you can scale up the loading of the rating vehicle. If your rating factor is 2.0, you should be able to put a vehicle on the bridge that weighs double. But, say your rating vehicle give V* = 1000 kN and (phi.Vu - V*g) = 2000 kN under that loading: RF appears to be 2.0. However, reanalyse for double the load: V* = 2000 kN but (phi.Vu - V*g) is now only 1800 kN. You weren't able to double the rating vehicle. I believe this is what the article is getting at.
- Thread starter
- #9
Hello steveh49,
Response to your second comment.
I was referring to a new bridge and using the same vehicle,i.e. design_vehicle = rating_vehicle, and the use of the same set of design standards. The general expectation is V_u(design) = V_u(load rating). Quite often road authorities require new bridges to be load rated.
For an old bridge they can be different even for the same vehicle owing to deterioration in the bridge since constructed, the availability of better information etc. So it is possible for the capacity to be different if I design a new bridge now and load rate it 50 years later using the same set of design standards.
Response to your second comment.
I was referring to a new bridge and using the same vehicle,i.e. design_vehicle = rating_vehicle, and the use of the same set of design standards. The general expectation is V_u(design) = V_u(load rating). Quite often road authorities require new bridges to be load rated.
For an old bridge they can be different even for the same vehicle owing to deterioration in the bridge since constructed, the availability of better information etc. So it is possible for the capacity to be different if I design a new bridge now and load rate it 50 years later using the same set of design standards.
Settingsun
Structural
That expectation needs to be tempered by the fact that shear capacity is no longer independent of the loading. The current (MCFT) code can give you 2000 kN capacity on paper, but is subject to the fine print that 2000 kN is the capacity only as long as you never try to use it. If you don't iterate, all you've got is a pass/fail result and not a true capacity.
BTW, QMR was rating the bridges as-new. They were just using a different method for load rating than for new design.
BTW, QMR was rating the bridges as-new. They were just using a different method for load rating than for new design.
Settingsun
Structural
Maybe there's more going on. The results for Cross Section 2 don't make sense to me at first glance. Using V*=374, the authors apparently got Vu=556.3. It's not clear whether they're iterating to make V* match Vu or match phi.Vu but, in either case, shouldn't the iterated capacity be more than the trial V*? They get it going down substantially.
If they were matching phi.Vu (which is the right way IMO), V*=374 resulted in phi.Vu=389. They almost match already. Iteration should do little.
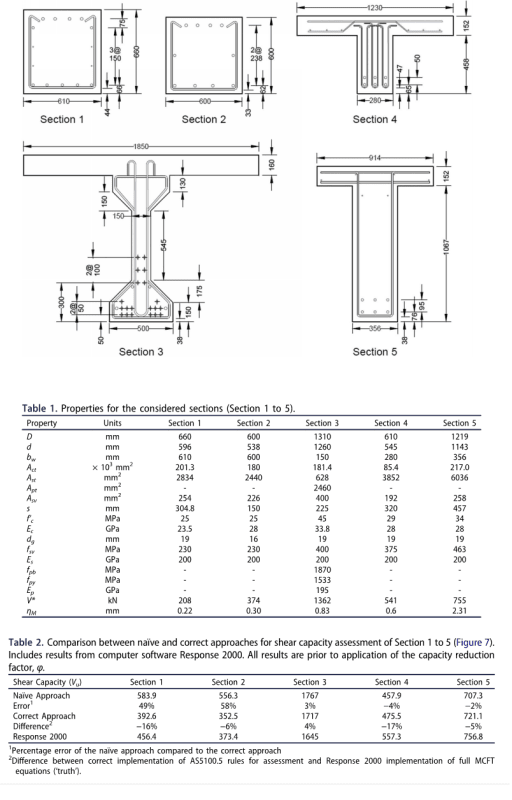
If they were matching phi.Vu (which is the right way IMO), V*=374 resulted in phi.Vu=389. They almost match already. Iteration should do little.

Settingsun
Structural
Here's a couple of figures from the paper that show the guts of what they're trying to do.
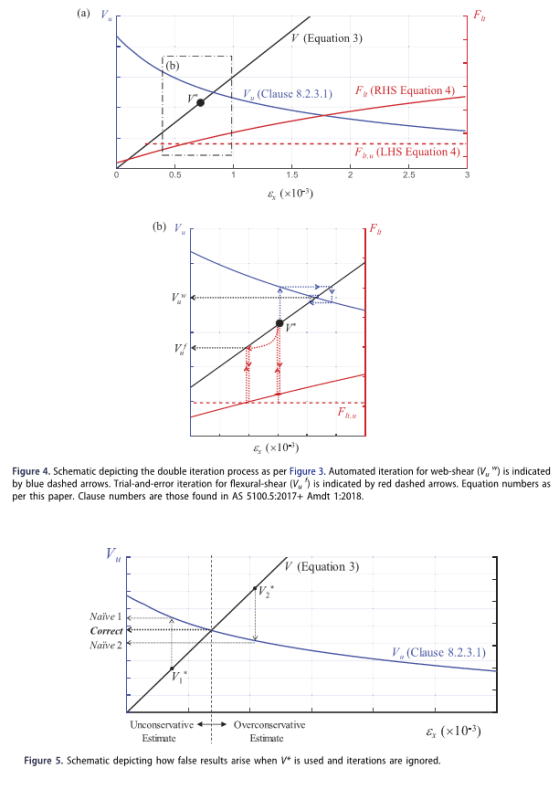

- Thread starter
- #13
Hello stevenh49,
Load rating of shear without the use of the proposed approach is useful as the rating can give an indication of relative shear carrying capacity of different bridges in the network for the same rating vehicle. The rating conforms to MCFT. Load rating by the modified approach using Vu(approach) and V*(AS 5100.7) does not conform to MCFT so is not suitable to use for the purpose stated in the first sentence.
Since MCFT uses strength that is a function of several load effects and many of the equations used have non-linear terms, care must be taken in coming up with a procedure for load rating and how to use the information obtained. See the comment from Holt et al about taking care in using load rating results.
"A typical MCFT-based shear-moment interaction diagram for a generic section is provided in Figure CB5.2-6 of the current LRFD Bridge Design Specifications, which shows non-linearity over the range of applied moments. This figure should remind load rating engineers that simple linear ratios in capacity, and hence rating factors, may give incorrect results."
page 91 of report
Holt, J., Garcia, U., Waters, S., Monnopolis, C., Zhu, A., Bayrak, O., Powell, L., Halbe, K.,Kumar, P., and Chavel, B. (2018). Concrete bridge shear load rating, Synthesis report.U.S. Department of Transport Federal Highway Administration, November
In previous standards where is shear capacity is not dependent on other action effects, the type of logic you described can be used as the capacity is more or less invariant. With MCFT, the ratio (phi.Vu - V*g) is not constant with changes in loading. This is a non-linear problem and ideally a rigorous assessment procedure (e.g. building load rating into structural analysis programs) should be used for heavy vehicle movement assessment.
Also, I do not think the use of the assumed proportional loading of load effects to give V*(approach)= Vu(approach) is useful.
The approach results in the following:
A new shear capacity Vu (approach) as been obtained for a system (bridge and load rating vehicle) x Vu(approach)/V*(AS 5100.7), since load and other safety factors should not be scaled. This capacity is not suitable for calculating LR for the nominated rating vehicle on the bridge since it uses a strength that is not consistent with the applied loading. Note that if Vu(approach)/V*(AS 5100.7) is less than unity, the dead and permanent load has been scaled down as well !!
My opinion is that the correct way to present the outcome caused by using the proposed approach is as below (to enable conformation to MCFT).
Clearly states that the load rating is for a bridge vehicle system with the dead and live load both multiplied by a factor Vu(approach)/V*(AS 5100.7) where V*(AS5100.7) is the factored shear of AS 5100.7.
The load rating factor LR is to be calculated as
phiVu(approach) - [V*(DL)(AS5100.7) x Vu(approach)/V*(AS 5100.7)]
---------------------------------------------------------
V*(LL)(AS5100.7) x Vu(approach)/V*(AS 5100.7)
Usefulness of the approach?
Load rating of shear without the use of the proposed approach is useful as the rating can give an indication of relative shear carrying capacity of different bridges in the network for the same rating vehicle. The rating conforms to MCFT. Load rating by the modified approach using Vu(approach) and V*(AS 5100.7) does not conform to MCFT so is not suitable to use for the purpose stated in the first sentence.
Since MCFT uses strength that is a function of several load effects and many of the equations used have non-linear terms, care must be taken in coming up with a procedure for load rating and how to use the information obtained. See the comment from Holt et al about taking care in using load rating results.
"A typical MCFT-based shear-moment interaction diagram for a generic section is provided in Figure CB5.2-6 of the current LRFD Bridge Design Specifications, which shows non-linearity over the range of applied moments. This figure should remind load rating engineers that simple linear ratios in capacity, and hence rating factors, may give incorrect results."
page 91 of report
Holt, J., Garcia, U., Waters, S., Monnopolis, C., Zhu, A., Bayrak, O., Powell, L., Halbe, K.,Kumar, P., and Chavel, B. (2018). Concrete bridge shear load rating, Synthesis report.U.S. Department of Transport Federal Highway Administration, November
In previous standards where is shear capacity is not dependent on other action effects, the type of logic you described can be used as the capacity is more or less invariant. With MCFT, the ratio (phi.Vu - V*g) is not constant with changes in loading. This is a non-linear problem and ideally a rigorous assessment procedure (e.g. building load rating into structural analysis programs) should be used for heavy vehicle movement assessment.
Also, I do not think the use of the assumed proportional loading of load effects to give V*(approach)= Vu(approach) is useful.
The approach results in the following:
A new shear capacity Vu (approach) as been obtained for a system (bridge and load rating vehicle) x Vu(approach)/V*(AS 5100.7), since load and other safety factors should not be scaled. This capacity is not suitable for calculating LR for the nominated rating vehicle on the bridge since it uses a strength that is not consistent with the applied loading. Note that if Vu(approach)/V*(AS 5100.7) is less than unity, the dead and permanent load has been scaled down as well !!
My opinion is that the correct way to present the outcome caused by using the proposed approach is as below (to enable conformation to MCFT).
Clearly states that the load rating is for a bridge vehicle system with the dead and live load both multiplied by a factor Vu(approach)/V*(AS 5100.7) where V*(AS5100.7) is the factored shear of AS 5100.7.
The load rating factor LR is to be calculated as
phiVu(approach) - [V*(DL)(AS5100.7) x Vu(approach)/V*(AS 5100.7)]
---------------------------------------------------------
V*(LL)(AS5100.7) x Vu(approach)/V*(AS 5100.7)
Usefulness of the approach?
- Thread starter
- #14
Steveh49. It is difficult to follow the numbers in the paper. I did not try to do that. I can follow the approach since I have been looking into this for the last few years with a research collaborator. No sure why there is a need to use the proposed approach. Please see my posting before this as to what I think the approach does.
Settingsun
Structural
I would discuss this with the person who procured the load rating to make sure it does what they want. Main Roads engineers I dealt with used to interpret the rating factor as I said: how much can the vehicle load be increased. I think this could still be used to compare bridges on the network as you said, but there's definitely more than one approach now.
The issue that makes me pause is that the MCFT capacity is only on paper. It can't necessarily be used. Is it really the capacity that the numerator in the rating factor calls for? Scaling up the vehicle load doesn't match the definition of the denominator, but gives you a real numerator.
I didn't follow your comment about scaling the dead load.
The issue that makes me pause is that the MCFT capacity is only on paper. It can't necessarily be used. Is it really the capacity that the numerator in the rating factor calls for? Scaling up the vehicle load doesn't match the definition of the denominator, but gives you a real numerator.
I didn't follow your comment about scaling the dead load.
- Thread starter
- #16
See Figure 5 above. Let us assume that there is only two action effects V and M. What does the line represent ?
At the origin. V* (and the corresponding M*) is zero and P=0.
At the point V*2, the shear is V*2.as5100.7. The corresponding capacity is Naive2(as5100.7) and the corresponding moment is M*2.as5100.7. I added "as5100.7" to show that these are factored load effects of the full bridge vehicle system, say Pas5100.7. The coefficient etaM is calculated as M*2.as5100.7/V*2.as5100.7.
After using the assumed loading (which is not an actual loading) and the iterative solution procedure, the ultimate shear capacity is now Correct(proposed). the word "proposed" to show that it is from the proposed approach. The converged solution also gives a corresponding shear equals to Correct(proposed), since V=Vu at the intersecting point. As can be seen from the diagram for this scenario, the strength correspond to a reduced shear equals to Correct(proposed). We then relate the shear back to the loading. Since V*2.as5100.7 is the shear for the full system load and Correct(proposed) is the shear of the new strength, what is the loading in relation to this shear?
At origin the load is V=0, M=etaM x 0 =0, And load P=0
At V*2.as5100.7, the shear is V*2.as5100.7 and the moment is V*2.as5100.7 x etaM=M*2.as5100.7 . The load is Pas5100.7
At the intersection point, the shear is Correct(proposed), and the moment = eta_M*shear = eta_M* Correct(proposed).
The load is P x Correct(proposed)/ Pas5100.7
So the capacity thus obtained is for a loading = full load system Pas5100.7 scaled by a factor Correct(proposed)/as5100.7.
For this scenario, it is < 1.0
At the origin. V* (and the corresponding M*) is zero and P=0.
At the point V*2, the shear is V*2.as5100.7. The corresponding capacity is Naive2(as5100.7) and the corresponding moment is M*2.as5100.7. I added "as5100.7" to show that these are factored load effects of the full bridge vehicle system, say Pas5100.7. The coefficient etaM is calculated as M*2.as5100.7/V*2.as5100.7.
After using the assumed loading (which is not an actual loading) and the iterative solution procedure, the ultimate shear capacity is now Correct(proposed). the word "proposed" to show that it is from the proposed approach. The converged solution also gives a corresponding shear equals to Correct(proposed), since V=Vu at the intersecting point. As can be seen from the diagram for this scenario, the strength correspond to a reduced shear equals to Correct(proposed). We then relate the shear back to the loading. Since V*2.as5100.7 is the shear for the full system load and Correct(proposed) is the shear of the new strength, what is the loading in relation to this shear?
At origin the load is V=0, M=etaM x 0 =0, And load P=0
At V*2.as5100.7, the shear is V*2.as5100.7 and the moment is V*2.as5100.7 x etaM=M*2.as5100.7 . The load is Pas5100.7
At the intersection point, the shear is Correct(proposed), and the moment = eta_M*shear = eta_M* Correct(proposed).
The load is P x Correct(proposed)/ Pas5100.7
So the capacity thus obtained is for a loading = full load system Pas5100.7 scaled by a factor Correct(proposed)/as5100.7.
For this scenario, it is < 1.0
kww2008 said:Hello Doug. The link of the published AJSE article is provided below. The article recommended that this approach be included in AS 5100.7 for shear load rating. The other papers publications referred to this article.
Thanks, I did have a look at the issues raised in the article some time ago. I'll have a re-read and read discussion above to see if I have anything to add.
Doug Jenkins
Interactive Design Services
- Thread starter
- #18
Doug,
Thank you Doug.
Please note that it was stated in the paper that "iteration is required for capacity assessment as discussed in various publications such as Collins and Mitchell (2014)". The capacity assessment in the paper by Collins and Mitchell was carried out to determine shear strength at failure of a test structure subjected to monotonically increasing load to failure. Since the shear strength at failure where Vn=Vu is not known beforehand an iterative solution search procedure had to be used. The loading assumed in the analysis characteristic was used in the calculation. Such iterative solution search procedures are commonly to predict MCFT-based shear strength of test structures tested to collapse. For example, an iterative solution search procedure (sort of) was used in the study by Rajakaruna, Vanisssorn and Wong for the prediction of failure shear strengths of bridge beams tested in the laboratory.
(link:
On the other hand, shear strength determination to AS 5100.7 is different as the loading is for a bridge with a moving rating vehicle. At any instance of loading, the ultimate capacity can be calculated directed from the corresponding load effects. No iteration is required. Also, the loading is not progressively increased to cause collapse.
Thank you Doug.
Please note that it was stated in the paper that "iteration is required for capacity assessment as discussed in various publications such as Collins and Mitchell (2014)". The capacity assessment in the paper by Collins and Mitchell was carried out to determine shear strength at failure of a test structure subjected to monotonically increasing load to failure. Since the shear strength at failure where Vn=Vu is not known beforehand an iterative solution search procedure had to be used. The loading assumed in the analysis characteristic was used in the calculation. Such iterative solution search procedures are commonly to predict MCFT-based shear strength of test structures tested to collapse. For example, an iterative solution search procedure (sort of) was used in the study by Rajakaruna, Vanisssorn and Wong for the prediction of failure shear strengths of bridge beams tested in the laboratory.
(link:
On the other hand, shear strength determination to AS 5100.7 is different as the loading is for a bridge with a moving rating vehicle. At any instance of loading, the ultimate capacity can be calculated directed from the corresponding load effects. No iteration is required. Also, the loading is not progressively increased to cause collapse.
I think the previous responses answered this well.
The shear strength of a beam is the shear strength of a beam. It does not care what loads are applied to it.
The MCFT will overestimate the shear strength if the applied loads are less than the capacity, because you are determining the capacity based on a combination of loads that are not actually present when the beam is at the brink of shear failure. The loads definitely need to be scaled up proportionally, which will bring the capacity down, and meet somewhere in the middle. Think about a situation where the applied loads are effectively zero; you will end up with a much larger capacity than if the loading was greater, which makes no sense. The capacity should not depend on the loads that are applied.
On the other hand, the MCFT will underestimate the shear strength if the applied loads are greater than the capacity, which would happen for things like load capacity assessments of bridges where we are determining the load rating for a heavy truck. In this case, there is additional capacity to be squeezed out of the model by scaling down the loads to the point where the beam is at the brink of shear failure.
The shear strength of a beam is the shear strength of a beam. It does not care what loads are applied to it.
The MCFT will overestimate the shear strength if the applied loads are less than the capacity, because you are determining the capacity based on a combination of loads that are not actually present when the beam is at the brink of shear failure. The loads definitely need to be scaled up proportionally, which will bring the capacity down, and meet somewhere in the middle. Think about a situation where the applied loads are effectively zero; you will end up with a much larger capacity than if the loading was greater, which makes no sense. The capacity should not depend on the loads that are applied.
On the other hand, the MCFT will underestimate the shear strength if the applied loads are greater than the capacity, which would happen for things like load capacity assessments of bridges where we are determining the load rating for a heavy truck. In this case, there is additional capacity to be squeezed out of the model by scaling down the loads to the point where the beam is at the brink of shear failure.
-
1
- #20
I think the original issue, about whether to iterate or not, has been resolved. If you want to find the actual shear capacity for a given ratio of moment to shear, you need to iterate. If you have a defined required shear capacity (and associated moment), you don't need to, but it makes sense to do it anyway because you'll be doing the calculation on a computer, so the iteration is negligible extra effort, and it gives you better information about the actual capacity of the section.
But there are outstanding issues, the main one being related to:
I don't think I agree with that (but perhaps I don't correctly understand how it would be implemented). The main problem I see with it is in calculation of the additional load on the longitudinal steel.
The procedure (I think) complies with the code is:
- Find Vuc and Vus by iteration (with no phi factor applied)
- Find the area of longitudinal steel required for the additional longitudinal force.
- Find the unfactored moment capacity of the section (Mu) with the reduced longitudinal steel area.
- If phim.Mu < M* then adjust V (section total unfactored shear capacity), and the associated M, by iteration so that Mu = M
- Then phiv.Vu = phiv.V and phim.Mu = phim.M
Certainly the code is not clear about the procedure for the case where the shear capacity is controlled by the longitudinal steel, and the recent supplement to AS 3600 is not helpful, it basically says just follow the code.
Also I doubt that the following statement from AS 3600 Supplement is always true:
C8.2.8 Proportioning longitudinal reinforcement
...
Alternatively, for reinforced concrete members subjected solely to bending and shear stress resultants, it is conservative to extend the longitudinal reinforcement needed to resist flexure alone by a distance of dv.cot(Thetav) past the section where it is theoretically no longer required for bending, in the direction of increasing shear.
Note that the code Cl 8.2.8 also requires there are "no sudden changes in the calculated tension force", but this is not mentioned in the supplement.
Doug Jenkins
Interactive Design Services
But there are outstanding issues, the main one being related to:
steveh49 said:If they were matching phi.Vu (which is the right way IMO), V*=374 resulted in phi.Vu=389.
I don't think I agree with that (but perhaps I don't correctly understand how it would be implemented). The main problem I see with it is in calculation of the additional load on the longitudinal steel.
The procedure (I think) complies with the code is:
- Find Vuc and Vus by iteration (with no phi factor applied)
- Find the area of longitudinal steel required for the additional longitudinal force.
- Find the unfactored moment capacity of the section (Mu) with the reduced longitudinal steel area.
- If phim.Mu < M* then adjust V (section total unfactored shear capacity), and the associated M, by iteration so that Mu = M
- Then phiv.Vu = phiv.V and phim.Mu = phim.M
Certainly the code is not clear about the procedure for the case where the shear capacity is controlled by the longitudinal steel, and the recent supplement to AS 3600 is not helpful, it basically says just follow the code.
Also I doubt that the following statement from AS 3600 Supplement is always true:
C8.2.8 Proportioning longitudinal reinforcement
...
Alternatively, for reinforced concrete members subjected solely to bending and shear stress resultants, it is conservative to extend the longitudinal reinforcement needed to resist flexure alone by a distance of dv.cot(Thetav) past the section where it is theoretically no longer required for bending, in the direction of increasing shear.
Note that the code Cl 8.2.8 also requires there are "no sudden changes in the calculated tension force", but this is not mentioned in the supplement.
Doug Jenkins
Interactive Design Services
- Status
- Not open for further replies.
Similar threads
- Question
- Replies
- 1
- Views
- 10K
- Locked
- Question
- Replies
- 21
- Views
- 2K
- Locked
- Question
- Replies
- 29
- Views
- 5K
- Replies
- 0
- Views
- 467
- Locked
- Question
- Replies
- 6
- Views
- 2K
