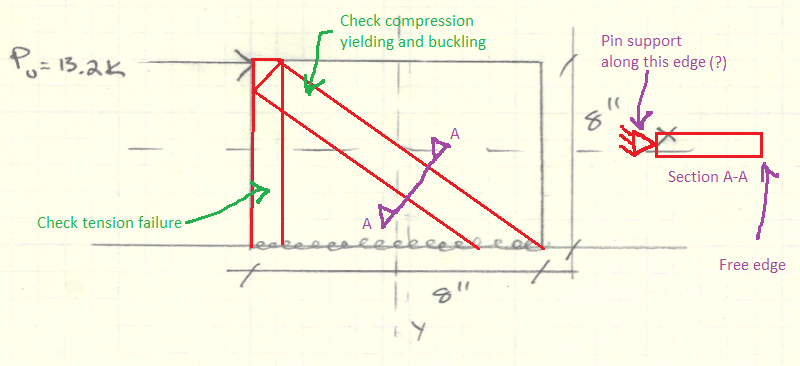
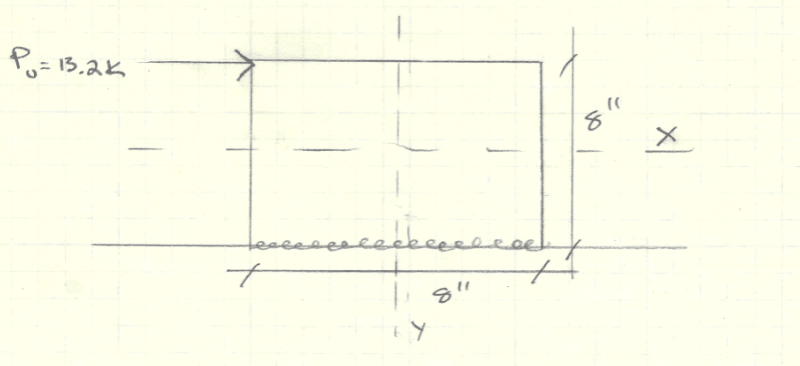
I have a 1/2" cantilevered steel plate welded to a steel beam. The plate is experiencing a 13 kip load as shown in the image below:
My question is, can I use AISC 14th F11. RECTANGULAR BARS AND ROUNDS and apply those equations to calculate flexural strength? My understanding was that bars are different than plates, even though they both have rectangular sections.
Can anyone provide structural theory that can justify it? I have seen some explanations on here talking about the Z/S ratio.
At work, I am being told to just check (phi)Mn = Fy*S, and I also want to know whether it is reasonable to assume that the plate can get to the plastic moment without buckling or other modes of failure?

My question is, can I use AISC 14th F11. RECTANGULAR BARS AND ROUNDS and apply those equations to calculate flexural strength? My understanding was that bars are different than plates, even though they both have rectangular sections.
Can anyone provide structural theory that can justify it? I have seen some explanations on here talking about the Z/S ratio.
At work, I am being told to just check (phi)Mn = Fy*S, and I also want to know whether it is reasonable to assume that the plate can get to the plastic moment without buckling or other modes of failure?

![[pipe] [pipe] [pipe]](/data/assets/smilies/pipe.gif)