Hi all,
I have a simple mechanics of solids type question which I have been googling, but I have not been able to find an answer.
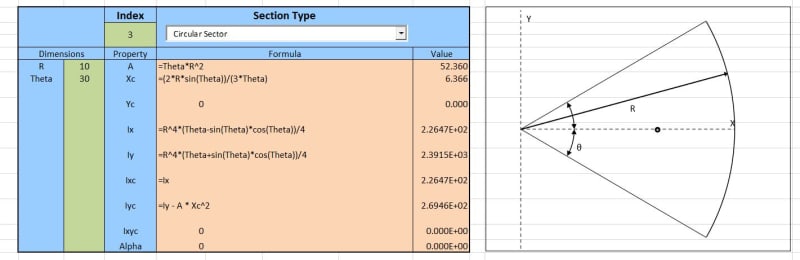
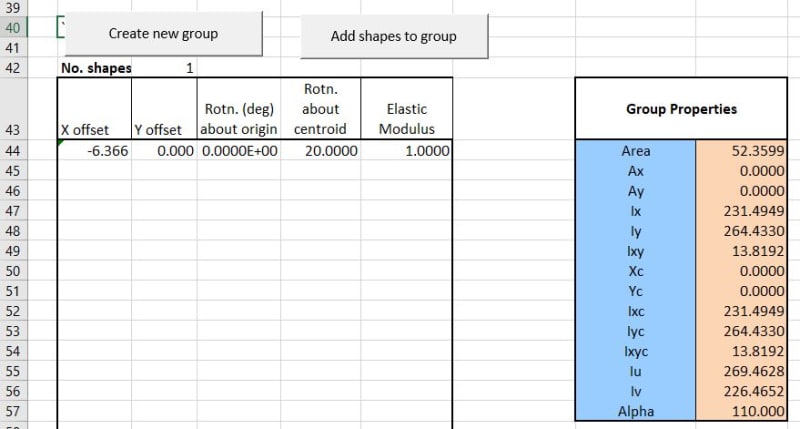
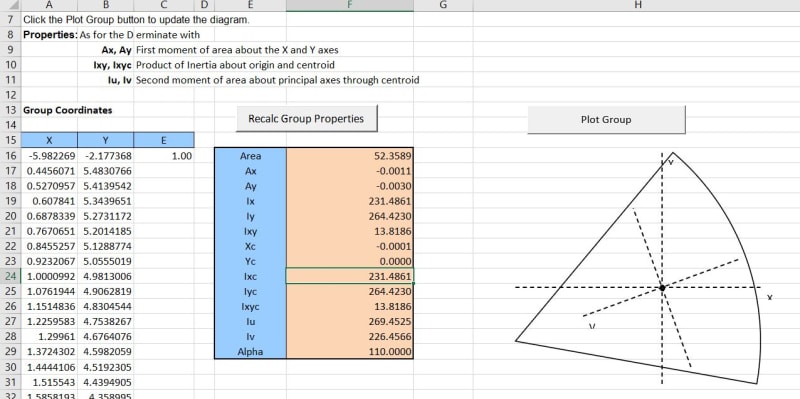
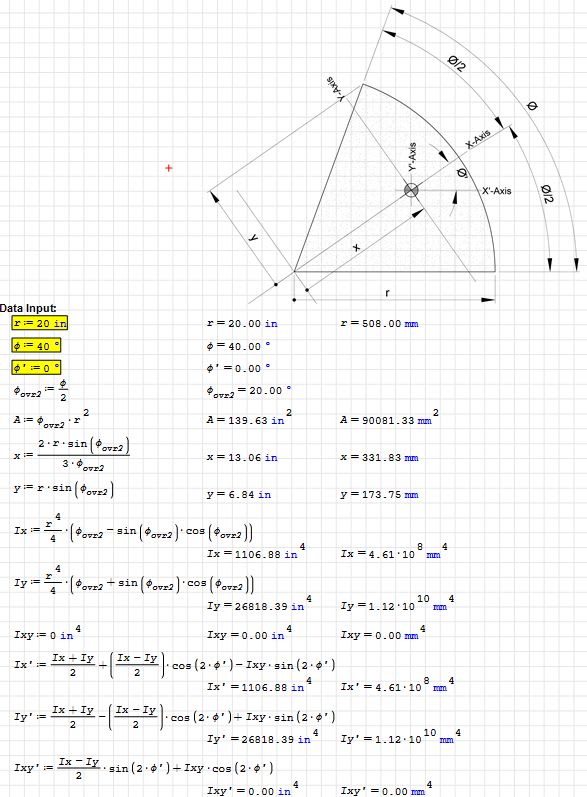
I have an irregular shaped section with bending moments imposed about its X axis as shown below.
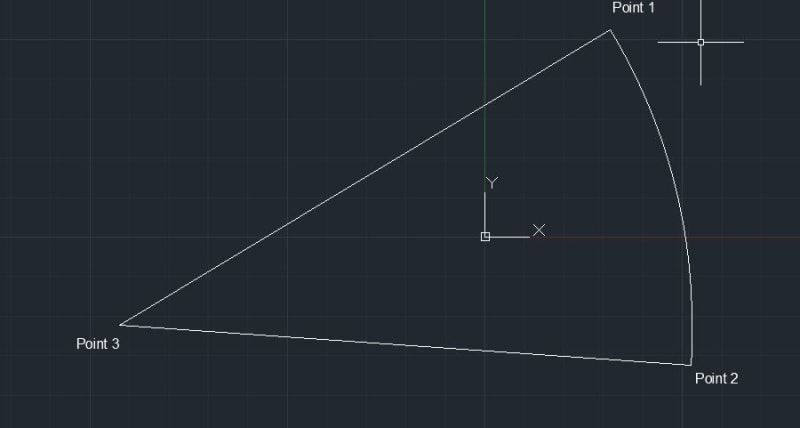
The centroid of the shape coincide with the x=0 aand y = 0 of the co-ordinate system.
Now for me to check my bending stresses at point 1 , 2 and 3, I need calculate my section modulus about Section X for each of these points.
If this was a simple rectangle, we could simply use B * H^2/6.
Is there any formular which would let me calculate the corresponding section modulus for these three points if I provide co-ordinates and Ix, Iy and Ixy values which I cam get of Autocad.
For context, I am trying model a deteriorated timber pile to check load capacity.
Any help would be appreciated.
Cheers,
Dimuth
I have a simple mechanics of solids type question which I have been googling, but I have not been able to find an answer.
I have an irregular shaped section with bending moments imposed about its X axis as shown below.

The centroid of the shape coincide with the x=0 aand y = 0 of the co-ordinate system.
Now for me to check my bending stresses at point 1 , 2 and 3, I need calculate my section modulus about Section X for each of these points.
If this was a simple rectangle, we could simply use B * H^2/6.
Is there any formular which would let me calculate the corresponding section modulus for these three points if I provide co-ordinates and Ix, Iy and Ixy values which I cam get of Autocad.
For context, I am trying model a deteriorated timber pile to check load capacity.
Any help would be appreciated.
Cheers,
Dimuth



![[pipe] [pipe] [pipe]](/data/assets/smilies/pipe.gif)