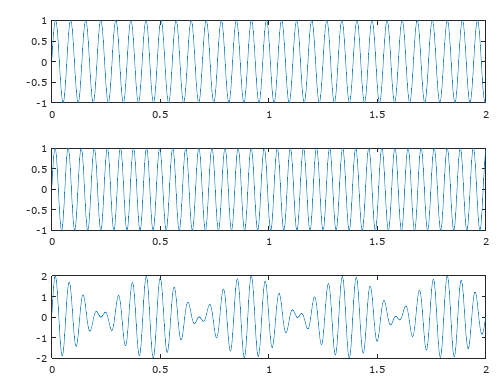
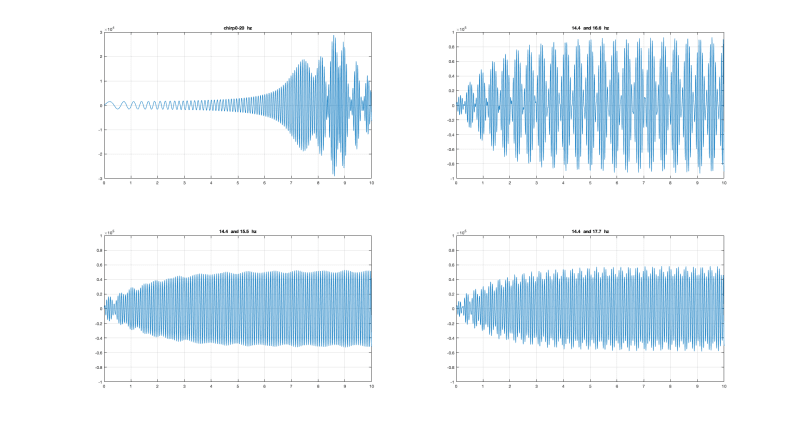
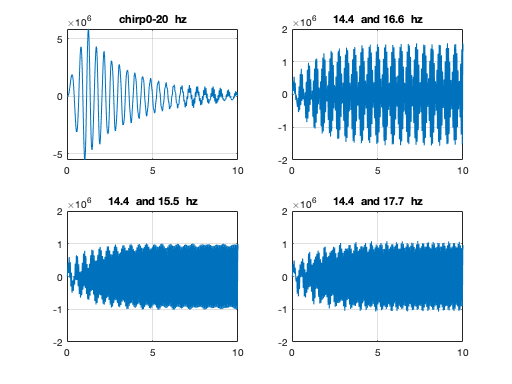
I have a structure with two vibrating screens (14.4 Hz and 16.6 Hz) they are on separate levels but share columns. We are having a lot of trouble with one screen but no one has been able to find vibration reading that show a problem. My question is how do the vibration forces combine from two different pieces of vibrating equipment? I have read about beat frequencies but that seemed very specific to audio frequencies. Plus (as I understand beat frequencies) it would be 16.6-14.4=2.2 Hz. When I do FFT from my field reading I don't see anything in this area. I am recording 59 seconds of data so it seems like I should collect several instances of a 2.2 Hz signal.
Is it possible the two signals could peak at the same time but infrequently? I am wondering if that is happening and sending a shock wave through the structure but it just hasn't been captured in recording data yet.
FFT's shows strongest reading at the machine vibrating frequency. So that gives me confidence my data collection and analysis is ok.
The machine supplier has said the structure is at fault but they haven't shared their data or said that some parameter is out of spec.
Is it possible the two signals could peak at the same time but infrequently? I am wondering if that is happening and sending a shock wave through the structure but it just hasn't been captured in recording data yet.
FFT's shows strongest reading at the machine vibrating frequency. So that gives me confidence my data collection and analysis is ok.
The machine supplier has said the structure is at fault but they haven't shared their data or said that some parameter is out of spec.