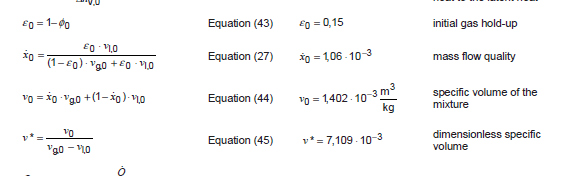Hello to all,
We are calculating PSV for two phase scenario and we have noticed that the mass quality fraction (x0) is too low, about 0.0006, that mean that from 100 kg/h 99.9994 kg/h are liquid and only 0.0006 kg/h are vapor.
On Fundamental Equations for Two-Phase Flow in Tubes - Masahiro Kawaji the definition of the mass flow quality is:
x0= mg / (mg + ml)
where:
On the other hand, the ISO 4126-10 (sorry I can't put the link there) the definition of the mass flow quality is literally: Ratio of gas mass flow rate to total mass flow rate and the equation is:
x0 = e0· sv-l / ((1 - e0) · sv-g + e0 · sv-l)
where:
The first we notice is that is that the equation is reversed from the one explained in the book and also the text from the ISO Ratio of gas mass flow rate to total mass flow rate. In the ecuation of the ISO is referred to the liquid phase.
And this is even more puzzling, they multiply the sv-l with the void fraction. We do not undestant that because the void fraction has to be multiplied by the gas phase...
All of this give us a x0=0.0006 for a 99% full reactor for Ethyl Acetate, we think it makes no sense.
We propose change the equation for this one referred to the literature:
x0 = e0 · sv-g / (e0 · sv-g + (1 - e0) · sv-l)
That have more sense, whit that change we calculated that we have when the reactor is 99% full a 65% gas phase flow rate and when is 80% full a 98% gas phase flow rate, that is logical becouse if the reactor is 20% empty the liquid will not arrive to the PSV...
So, what do you think about that??? do you have any recommendation? do you have the same results?
We are calculating PSV for two phase scenario and we have noticed that the mass quality fraction (x0) is too low, about 0.0006, that mean that from 100 kg/h 99.9994 kg/h are liquid and only 0.0006 kg/h are vapor.
On Fundamental Equations for Two-Phase Flow in Tubes - Masahiro Kawaji the definition of the mass flow quality is:
x0= mg / (mg + ml)
where:
mg is gas mass flow
ml is liquid mass flow
ml is liquid mass flow
On the other hand, the ISO 4126-10 (sorry I can't put the link there) the definition of the mass flow quality is literally: Ratio of gas mass flow rate to total mass flow rate and the equation is:
x0 = e0· sv-l / ((1 - e0) · sv-g + e0 · sv-l)
where:
e0 is the void fraction in the pressurized system at sizing conditions - in other words, the percentage of the reactor's upper empty zone. e0=(1-filling level)
sv-l is the specific volume of the liquid
sv-g is the specific volume of the gas
sv-l is the specific volume of the liquid
sv-g is the specific volume of the gas
The first we notice is that is that the equation is reversed from the one explained in the book and also the text from the ISO Ratio of gas mass flow rate to total mass flow rate. In the ecuation of the ISO is referred to the liquid phase.
And this is even more puzzling, they multiply the sv-l with the void fraction. We do not undestant that because the void fraction has to be multiplied by the gas phase...
All of this give us a x0=0.0006 for a 99% full reactor for Ethyl Acetate, we think it makes no sense.
We propose change the equation for this one referred to the literature:
x0 = e0 · sv-g / (e0 · sv-g + (1 - e0) · sv-l)
That have more sense, whit that change we calculated that we have when the reactor is 99% full a 65% gas phase flow rate and when is 80% full a 98% gas phase flow rate, that is logical becouse if the reactor is 20% empty the liquid will not arrive to the PSV...
So, what do you think about that??? do you have any recommendation? do you have the same results?