> Hi guys i know its a very basic concept but i didnt quite understand this graph.
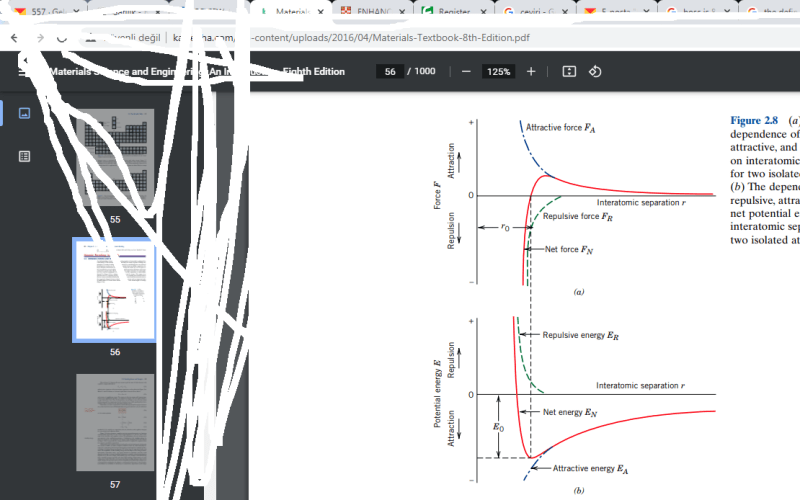
The two curves F (force) and E (energy) are related by differentiation or integration with respect to the spatial coordinate
something like
F = - d/dr (E)
E = - Int ( F ) dr + C
The negative sign to me means the force acts in direction opposite the r coordinate (i.e. positive F corresponds to attractive force within the system).
The force passes through zero where the slope of E is 0 (at a relative max or minimum of E).
As CP mentioned this is a minimum of potential energy, so it is a stable equilibrium (think about gravitational potential energy, then the curve is proportional to height and a ball rolling along the curve it will settle into that minimum and stay there).
> My confussion is when the distance beetween two atoms is R0 there is no net force applied on them but
how could still be a potential energy I thought that the potentail energy should be zero when the distance is R0 cause atoms dont want to move so they dont want to do work
Force is what we can measure and has an unambiguous physical significance.
Energy is a little more abstract and depends on that integration constant C which is somewhat arbitrary (or dependent upon whatever convention you use to define zero energy). These authors chose the convention where potential energy is zero when the atoms are at infinite distance. Positive potential energy at a given distance means you'd have to put energy into the 2-atom system to moved them from infinity to that distance. Negative potential energy at a given distance means you'd get energy out of the the 2-atom system if you moved them from infinity to that distance.
The equilibrium point (labeled as distance "r0") has a negative potential energy... i.e. you'd get energy (labeled as "R0") out of the system to move the atoms from infinite separation distance to distance r0. You'd have to put that same amount of energy back into the system to move them from r0 out to infinity, that amount of energy is sometimes labeled binding energy.
=====================================
(2B)+(2B)' ?