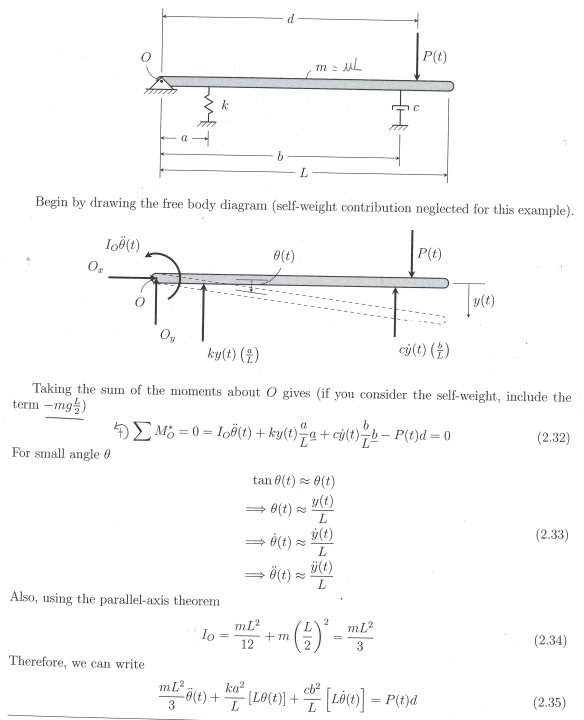
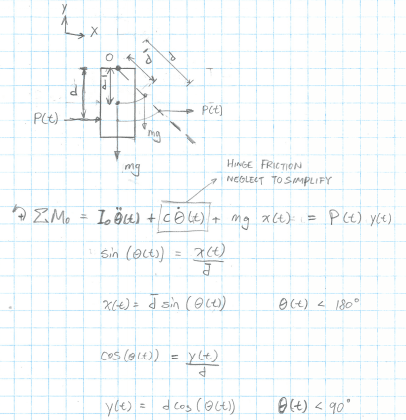
MegaStructures
Structural
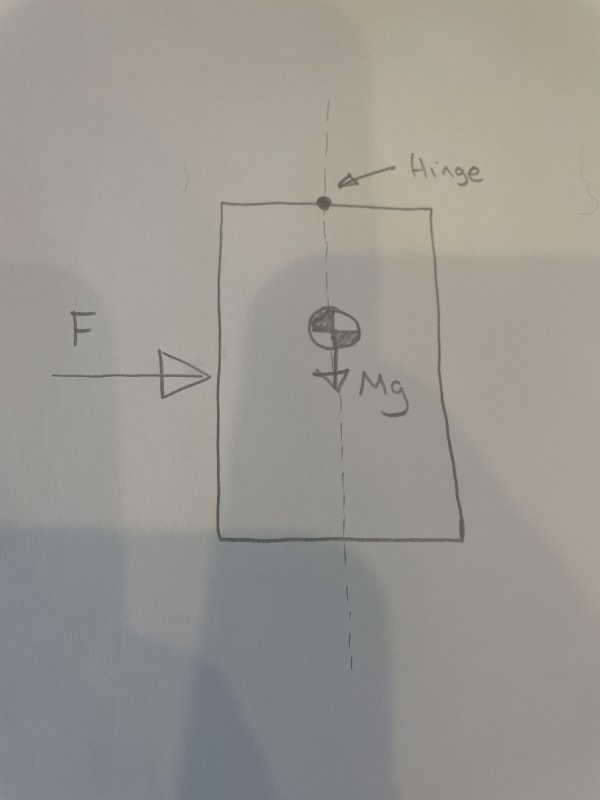
What would be the best way to calculate how far this object would rotate if a force acted on it for 3-seconds only?
“The most successful people in life are the ones who ask questions. They’re always learning. They’re always growing. They’re always pushing.” Robert Kiyosaki

“The most successful people in life are the ones who ask questions. They’re always learning. They’re always growing. They’re always pushing.” Robert Kiyosaki