Coulomb's Damping Equation for Machine Vibration
Coulomb's Damping Equation for Machine Vibration
(OP)
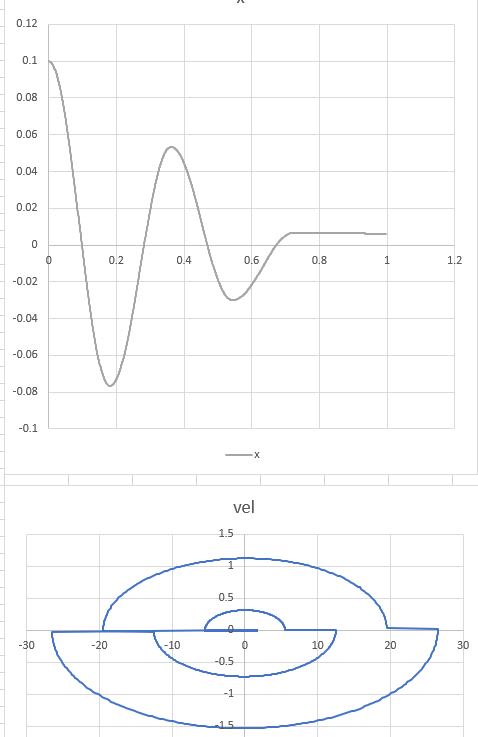
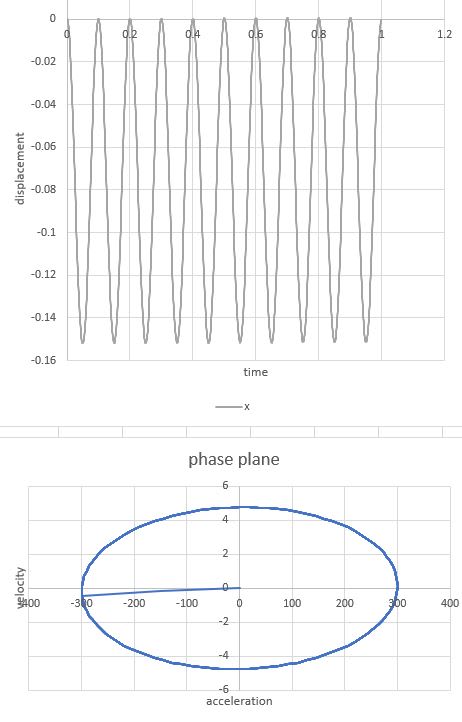
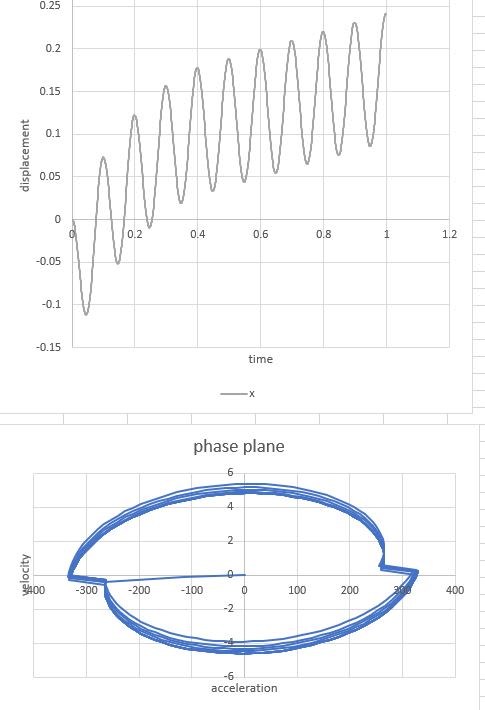
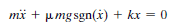I am working on a large industrial machine on frictional skid rails (i.e., 1 dimension of movement is possible on the rails). As its motor starts up, it begins to vibrate the machine around 20Hz; i.e., movement occurs on the frictional rails. The phenomenon is similar to what is shown in the YouTube video HERE. This is quite similar to Coulomb's damping scenario (images below).
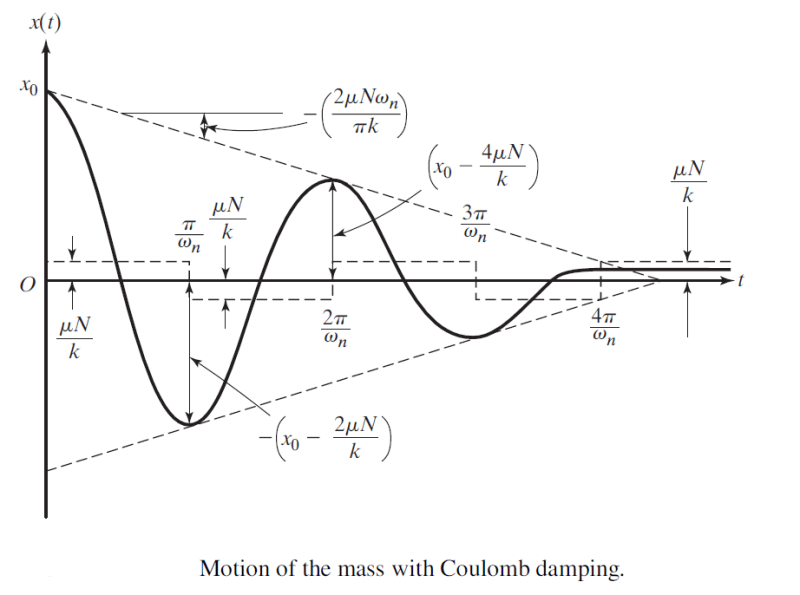
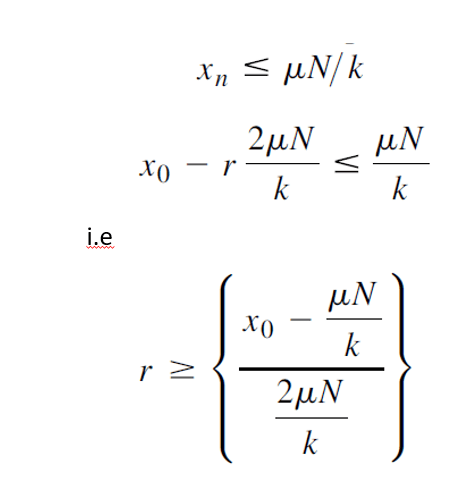
"r" is the number of half cycles that elapse before motion ceases. However, the equation assumes a spring participates in the situation (hence the variable "k"). It also assumes there is an initial displacement, x0 applied to the assembly. Neither the spring, nor the initial displacement occur in my scenario. Does anyone know how or if Coulomb's equation is modified to account for my scenario?
(note: yes, I understand an imbalance in the rotating assembly is likely the cause of the vibration and should be looked at. However, for all intents and purposes, we can assume in this conversation that the source of the vibration is there to stay. The structure and its motor are huge. So even a tiny imbalance may lead to large energy addition to the structure. With a free DOF along the skids, the energy may be enough to excite movement.)
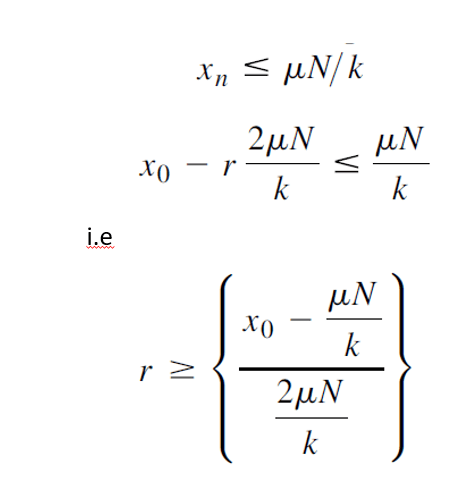
"r" is the number of half cycles that elapse before motion ceases. However, the equation assumes a spring participates in the situation (hence the variable "k"). It also assumes there is an initial displacement, x0 applied to the assembly. Neither the spring, nor the initial displacement occur in my scenario. Does anyone know how or if Coulomb's equation is modified to account for my scenario?
(note: yes, I understand an imbalance in the rotating assembly is likely the cause of the vibration and should be looked at. However, for all intents and purposes, we can assume in this conversation that the source of the vibration is there to stay. The structure and its motor are huge. So even a tiny imbalance may lead to large energy addition to the structure. With a free DOF along the skids, the energy may be enough to excite movement.)
Talk To Other Members
RE: Coulomb's Damping Equation for Machine Vibration
So the "large industrial machine" has it's rotating shafts oriented perpendicular to the rails?
And there are no wheels contacting the rails. Just skids?
https://www.abc.net.au/cm/rimage/11566802-1x1-larg...
Is the "vibration" accompanied by rigid body motion of the " large industrial machine" sliding/skidding along the rails,
A few picture of the arrangement would be at least as helpful as the lack of pictures is confusing.
RE: Coulomb's Damping Equation for Machine Vibration
I believe 60Hz is full speed. It was explained to me that 20Hz is a problem, but I cannot say for sure if it disappears above 20Hz.
I'm not sure. That information hasn't been disclosed.
Only skids. No wheels. You can imagine a ski on snow, except this is metal on metal.
Yes, it is similar to the YouTube video I shared. It moves rather violently in the direction of the skid rails.
I agree, but unfortunately I do not have them at the moment. The machine was shown to me, but I was not given photos to share.
Bottom line, I think FEA will be needed to simulate this, but I had hoped to get something meaningful with a hand calc of Coulomb's. If that's not possible, then I'll just revert to FEA.
RE: Coulomb's Damping Equation for Machine Vibration
https://www.bing.com/search?q=stick-slip+friction&...
Stick-slip phenomenon - Wikipedia
https://en.wikipedia.org/wiki/Stick-slip_phenomeno....
Walt
RE: Coulomb's Damping Equation for Machine Vibration
Let's be practical here.
That shop floor is not level. It is tilted downward and to the right, which is why the vibrating machine moves in that direction.
I figure the rubber mat does two things. It acts as a vibration isolator between the metal base and the floor. There is no clattering of the legs against the floor. If the vibration acceleration is well below 1G, there is lots of friction contact between the floor and the three‑legged base, so that it can't move.
Your vibration isolator reduces the vibration displacement and force transmitted to the floor. Effectively, it is providing a degree of freedom to the base and grinder above. The rubber mat increases the vibration movement of the grinder.
Vibration happens because you have mass, spring(s), and one or more forcing systems. Most of your springs could be your vibration isolators. If the forcing mechanism is continuous, the vibration does not die off. In a vibrating system, damping limits amplitude, and it transmits force.
What are your failure modes? If you don't want the machine to shake, you must attach it to something heavy, like your floor. Consider making your base very heavy. If you don't want to shake your building, you need anti-vibration mounts, and you need to live with your machine wiggling about.
--
JHG
RE: Coulomb's Damping Equation for Machine Vibration
From reading your reply, I believe you may be confused. My machine is not the grinder in the YouTube video. That was only a demonstrative video of a machine that manifests the phenomenon occurring in a large industrial machine I'm working with. In other words, it ramps up to full speed and induces vibration that leads to an ongoing stick-slip scenario. Coulomb's models this, but assumes some external initial perturbation, as well as a system elasticity.
RE: Coulomb's Damping Equation for Machine Vibration
I do not think I am confused. I discussed the grinder video you showed us, and I asked what your problem was.
If your machine is not solidly attached to your floor and it sees significant vibration, it will move around. If you don't want it to move around, it must stick and not slip. There is no external force on that grinder, so the only explanation for movement is that the floor is not perfectly level. Will your floor be perfectly level? Is any floor perfectly level?
Does your machine vibrate only while stopping and starting, or does it vibrate continuously? Perhaps 20Hz is close to a harmonic in your structure. Your Coulomb diagram seems to assume a dynamic event that starts and stops, possibly due to a single impulse. If your machine vibrates, you have a steady state condition of some kind.
If things are vibrating, you have a spring. That rubber pad the grinder is sitting on has a characteristic spring rate. If your machine is heavy, your spring could be stiff enough that you don't see it is a spring.
If your machine is sitting on slippery rails that are not perfectly level, it will move under vibration. The slippery rails possibly are springy.
What failure are you trying to prevent.
--
JHG
RE: Coulomb's Damping Equation for Machine Vibration
the problem is trivial to set up in a general sense:
The formulas you've shown are solutions to the homogenous equation
replace the zero on the rhs with your forcing function, which can be derived from the vibration profile of the unit. and solve for discrete time periods broken up by the direction of the oscillations (bc of the sgn function)...
... But I don't know how useful this would be for you - it seems like a long and tedious way of not directly solving the problem... And would be very difficult equation to solve if the motor vibrations are from a dynamic speed range and not steady state...
gl
RE: Coulomb's Damping Equation for Machine Vibration
The grinder guy mentions he moves the grinder stand around to various places and it moves to the right. He doesn't say "always" so that is unknown. It would be odd if the grinder orientation was always the same relative to the slope of the floor as a slight turn would cause it to come towards him or run away if slope was the only influence.
Aligning the induced motion with a slope will speed it up, but this has been seen on nearly perfectly level floors.
I'd like to see what happens if the grinder base was turned 15 degrees.
Coulomb's is not "stick-slip." If it was the friction force would show a sudden decrease, more of a stepped square wave. What that graph shows is a constant friction removing energy proportional to velocity until the energy is finally exhausted and the part stops off center. Notice in the diagram the friction component is constant and in opposition to the motion.
RE: Coulomb's Damping Equation for Machine Vibration
If you want help with a math problem, you'll have to define the math problem
If you want help with your machine, you'll have to explain the symptoms better.
At least that's where I stand. I have no clue what you're asking at this point.
fwiw I agree unlevel floor seems like a likely explanation for the grinder stand walking in the video but I don't think it's the only explanation. I can imagine for example a simple unbalance rotating force on a horizontal machine tends to exert up and down forces as well as horizontal side to side forces. The phase relationship of the forces is 90 degrees between the H and V but the phase relationship between the motion is not necessarily 90 degrees (there may be different proximity to resonance in the two directions). At any rate let's say the machine shaft is pointing E/W. The vertical motion may end up creating highest contact forces (and therefore friction) when the horizontal forces are pushing North and lowest contact forces (friction) when the horizontal forces are pushing south so the machine might ended up walk south. Now lets add grinding wheels on each end except they are tilted. The tilt will create a rotating moment which at certain times in the rotation will tend to push the machine below east and half a rotation later it will push the machine below west. Depending on how that aligns in time with the up/down force and associated contact friction, the machine might walk east/west in a direction of the shaft axis like in the video. Those are just very simple descriptions, actual machine behavior might be a lot more complex.
=====================================
(2B)+(2B)' ?
RE: Coulomb's Damping Equation for Machine Vibration
If the machine while operating is intended to remain at rest on skid without bolt/clamp attachments to the rails, then consider vibration isolation between machine base and skid rails.
Walt
RE: Coulomb's Damping Equation for Machine Vibration
The assembly is not supposed to move along the skids during motor operation. I believe the skids are used later when the motor is powered off.
It is not supposed to vibrate at all during motor operation. But the motor is triggering the assembly's natural frequency around 20Hz, leading to significant vibration along the frictional skids. Yes, shop measurements are being taken, but that data hasn't been shared with me yet. I agree that it seems a math equation (e.g., a variant of Coulomb's perhaps) does not exist.
Yes, isolation dampers are under consideration. Anything to increase the stiffness and shift the structure's natural frequency away from the motor's frequency.
We can all adjourn and move on elsewhere, if there's nothing more to add. I was only asking for a variant of Coulomb's equation, which now I don't think is available.
RE: Coulomb's Damping Equation for Machine Vibration
So going with trial and error:
- Put a weight on the machine. Maybe just increasing the contact force (from weight) on the rails will help.
- Move the weight around. Maybe the weight distribution of the skid is creating uneven loading at the rails.... imagine I have on top of the rails a flat plate with a structure welded on top in shape of a capital F with the weight in the horizontal bars of the F... then that weight puts a moment onto the bottom plate which may tend to lift or unload portions of the rails.
- Check the balance and alignment of the machine... correcting these things can reduce vibrations.
- Look for contaminants on the rails. Moisture, oil.
- Sure try damping if you want. Maybe throw a bag of sand on top. By the way what kind of a fix did you have in mind for damping... something between the rail surfaces like the rubber mat in the video? If you have access to that surface then trying various tape-on solutions or coating solutions might be worthwhile to change the surface characteristics. For that matter inspect the rails to see if they are flat, damaged. Or if you had something else in mind not between rail surfaces, I'd be curious to hear what you're picturing
By the way I'll say there is an amazing resource of knowledge on this forum. Greg Locock is a legend in vibration and related design stuff. TMoose knows his way around rotating machinery better than anyone else I know. Drawoh is a heckuva mechanical mind. Walt strong knows a whole lot about rotating machine vibration analysis. (That's not the limits of their knowledge, just what I remember about them.... and my apologies to anyone I omitted, these are just the guys I've learned from here). If you bring them more info, I'll bet they can give you some good ideas to solve your problem.=====================================
(2B)+(2B)' ?
RE: Coulomb's Damping Equation for Machine Vibration
I believe the "k" you are looking for resides inside the machine. It's not an external spring pushing/pulling the machine along the rails. The motor frequency excites an internal natural frequency. The large periodic forces developed moves the machine back and forth along the rails. The motion of the machine mimics the oscillating internal spring/mass/damper.
For the graph of the motion versus time you have in your original post, if you want the initial displacement to equal zero I believe you can just the shift the curve left or right till the displacement equals zero at time t=0.
RE: Coulomb's Damping Equation for Machine Vibration
This is wrong. OP shows formulas derived from a homogeneous (undriven) equation; you'd need to solve the same equation set equal to the forcing function (which is the driven vibration of the system).
See my above post for the characteristic equation governing the system, which is what you'd have to use to solve it analytically.
RE: Coulomb's Damping Equation for Machine Vibration
Yes, I believe you are correct. Your stated equation is the characteristic equation governing the system. I agree with your earlier post that it seems like a long and tedious approach. I guess I had hoped it would be fairly trivial to make a small tweak to "r" formula to generate the variant applicable to my scenario. It doesn't sound like it's that easy though.
RE: Coulomb's Damping Equation for Machine Vibration
onatirec is correct, though I would have expected a summation over all the individual masses and all their individual spring elements and all the internal and external damping coefficients and all the various excitation sources.
Th motor is putting energy into the system in complex ways and the way to understand that will be via complex equations.
See https://tigerprints.clemson.edu/all_theses/3149/ for an example to deal with a simplified solution.
RE: Coulomb's Damping Equation for Machine Vibration
Have there been additional recent measurements etc that have confirmed the motion of the "large industrial machine" is like the red block here -
https://www.youtube.com/watch?v=s3G3au-EyAQAre
Ignore the "fast return" speed variation.
Just Simple, pure Rigid body translation, with the red block sliding back and forth ( to and fro ?) on the blue rails.
And NO possibility the motion is actually the "large industrial machine" rocking because the rails are bending etc -
https://onlinelibrary.wiley.com/cms/asset/120d369e...
RE: Coulomb's Damping Equation for Machine Vibration
Something like:
m*d^2x/dt^2 + (mu)*m*g*F(t+phi)*sgn(dx/dt) + kx= F(t)
Where F(t) is really a collection of speed dependent excitations (e.g. e/m slotting, bearing frequencies, mechanical imbalances, etc) which are weighted by the structural resonances and produce effects roughly 90 degrees out of phase on each the normal force and force along the axis which it walks...
Very interesting problem, but you could probably write a dissertation on modelling and solving it analytically.
RE: Coulomb's Damping Equation for Machine Vibration
Checking the initial diagram
imbalance excitation, no friction
add coulomb friction. It walks!
Cheers
Greg Locock
New here? Try reading these, they might help FAQ731-376: Eng-Tips.com Forum Policies http://eng-tips.com/market.cfm?
RE: Coulomb's Damping Equation for Machine Vibration
You probably can't solve it analytically (ex laplace transform methods) because overcoming the static coefficient of friction represents a non-linearity. You need a numberical ODE solver (like ODE45 in matlab) which I presume most engineers have access to or can program themselves. Here's the simplest formulation I can come up with (just a starting point).
State variables Xv, Xh, Vv, Vh
where X is displacement, V is velocity, subscript h for horizontal, subscript v for vertical
The time derivatives of the state variables are as follows:
Xv' = Vv
Xh' = Vh
Vv' = [-K*Xv + Fub*cos(w*t)]/M
Vh' = [Fub*sin(w*t) +Friction]/M
where
Fub = Force magnitude (unbalance)
Ffriction = {K*Xv-M*g}*{Vh/|Vh|}{Mu_Static + (Mu_Dynamic-MuStatic)*f(|Vh|}}
...{K*Xv-M*g} represents the normal force.
...{Vh/|Vh|} gives the proper sign
...The third term in curly brackets { } will return either Mu_Static or Mu_Dynamic… ideally which one is returned depends on whether Vh = 0 or not but such an abrupt transition would cause instabilities in your numerical algorithm so it needs to be a smooth transition. The function be defined to satisfy conditions something like: f(0)=0, f'(0)=0, and f(TW)=1 f'(TW)=0 where TW is transition width and no abrupt changes in f or f'. Wide transition width favors numerical stability. Narrow transition width favors accuracy. You can build functions like this yourself. Edit: try using f(|Vh|)=0.5*(1-cos(pi*Vh/TW)) for |Vh|< TW, and f=1 for |Vh|> TW.
I may have made a sign error along the way somewhere… no guarantees. This is just first thought at how op could build a model for pure educational/entertainment purposes with no hope to do anything useful.
Edit - I didn't see Greg's post. I imagine he solved it with ode solver of some type in similar fashion to what I described. Also I didn't particularly notice until just now that op elects to ignore static coefficient of friction, that simplifies the problem to the point that it's linear and in theory it could be solved analytically.
=====================================
(2B)+(2B)' ?
RE: Coulomb's Damping Equation for Machine Vibration
Cheers
Greg Locock
New here? Try reading these, they might help FAQ731-376: Eng-Tips.com Forum Policies http://eng-tips.com/market.cfm?
RE: Coulomb's Damping Equation for Machine Vibration
1 - You probably used an ode solver. (i.e. time domain).
2 - op was allowing a simplified linear model of friction, which in theory permits analytical solution (a correction to my earlier comment that analytical solution wouldn't be possible).
=====================================
(2B)+(2B)' ?
RE: Coulomb's Damping Equation for Machine Vibration
Cheers
Greg Locock
New here? Try reading these, they might help FAQ731-376: Eng-Tips.com Forum Policies http://eng-tips.com/market.cfm?
RE: Coulomb's Damping Equation for Machine Vibration
Very interesting. Thanks for sharing!
I stopped reading your post here. I didn't come to this forum for snark, but for an educated discussion about the situation. Nowhere did I assertively indicate the problem MUST be solved analytically. In fact, to my surprise, I found myself more focused on keeping people in the thread on track, rather than discussing a wobbly YouTube bench grinder setting on a rubber floor mat (I felt like I was herding cats). I realize there are many unknowns, too many at this point. I realize it's a complicated problem. I merely thought I could apply the K.I.S.S. principal (keep it simple stupid) and uncover some slick approximate analytical method to roughly guide my troubleshooting. I wasn't hoping for a detailed, exact analytical equation to nail the situation perfectly. FEA will likely be the path forward.
RE: Coulomb's Damping Equation for Machine Vibration
If you put your pride aside and read further into my post, what I did was put the problem into a format suitable for solving by time domain simulation (ode solver) as Greg did. I made some assumptions along the way which I was prepared to discuss (*).... there is certainly room for tweaks to improve it. I spent about an hour organizing that because I was under the impression you wanted to try a numerical model and it seems like a good starting point to me. Low and behold, you liked the pretty pictures from Greg... but you went out of your way to explicitly reject my comments about how you might go about doing something similar yourself.
Humility is a virtue, whether in solving machinery problems or in asking for advice.
No worries. It's an interesting problem / discussion.
* Edit - discussion of my model for posterity:
- My K represented whatever stiffness / flexibility is below the modal mass
- Xv = 0 is the position where the mass rests on the spring under its own weight.
- The model assumes the machine never loses contact with the ground below it... you could certainly adapt the model to cover the case where the machine momentarily lifts off the support... this would give an adjustment to the Vv and Vh terms which applies when Xv is above a certain value
=====================================(2B)+(2B)' ?