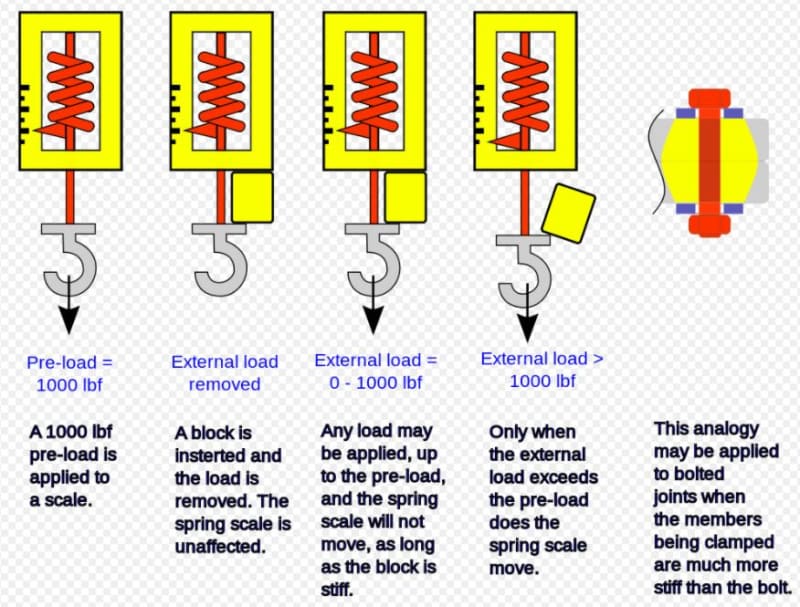
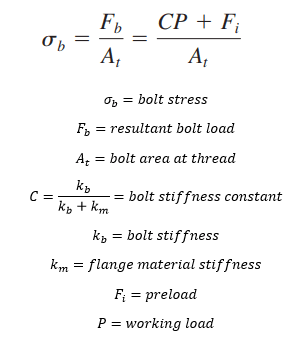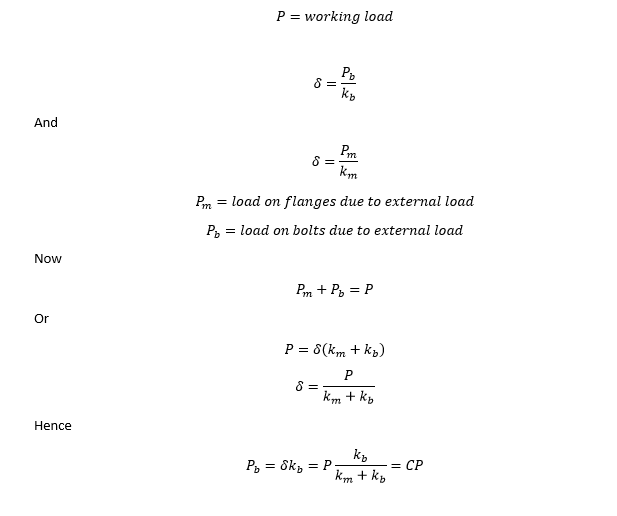Bolt load capacity after tightening 15

Nordic8 · Jan 8, 2021

Hi all,

I hope its not a stupid question, or if it is then maybe someone can point towards that "simple and obvious" answer that I'm failing to see here! Here goes:

I haven't got much experience with bolted joints, so far simple guidelines such as VDI2230 have helped me out just fine.

However, now I was trying to use VDI2230 for determining the tightening torques for a bolted flange and came across something that I fail to make sense of.

I'll give you a simplified description. It's a pipe with a flange, and an end cap bolted onto it to seal it off. Lets say it has 4 bolts that are evenly spread along the diameter, or 90degrees apart from each other. The holes in the flanges are not threaded, just bolts through and and nuts on the other side.

I'll use the VDI2230 method for calculating these bolts, following the procedure I found in a Würth publication.

Based on the diameter of the pipe and maximum working pressure I have determined that the maximum force on the cap will be 9.2 kN, that makes 2.3 kN per each of the 4 bolts. Therefore the axial operating force Fa = 2.3 kN.

As I have no shear forces to consider, the assembly preload force Fm = Fa = 2.3 kN. This will be my starting point.

Let's say I want to use grade 8.8 bolts. Looking at the VDI2230 table, the next closest load there is 2.5 kN -> size M4 is specified for 8.8 bolts.
Add one step for static concentric load -> 4.0 kN -> M5
Add one step for tightening with a torque wrench -> 6.3 kN -> M6

So the bolts that I need are grade 8.8 size M6.

I will estimate the coefficient of friction to be 0.11. The next closest step in the guidelines I have is 0.10, so lets got with that.

Based on all this, VDI2230 advises me that the tightening torque would be Ma = 9.0 Nm, which would create a 10.4 kN preload force in the bolt. It is said to utilize 90% of the screws yield strength.

Based on my calculation, the breaking load of a M6 8.8 coarse thread bolt at yield strength (640 MPa) is 11.29 kN.
10.4 / 11.29 = 92%, so that's just about right.

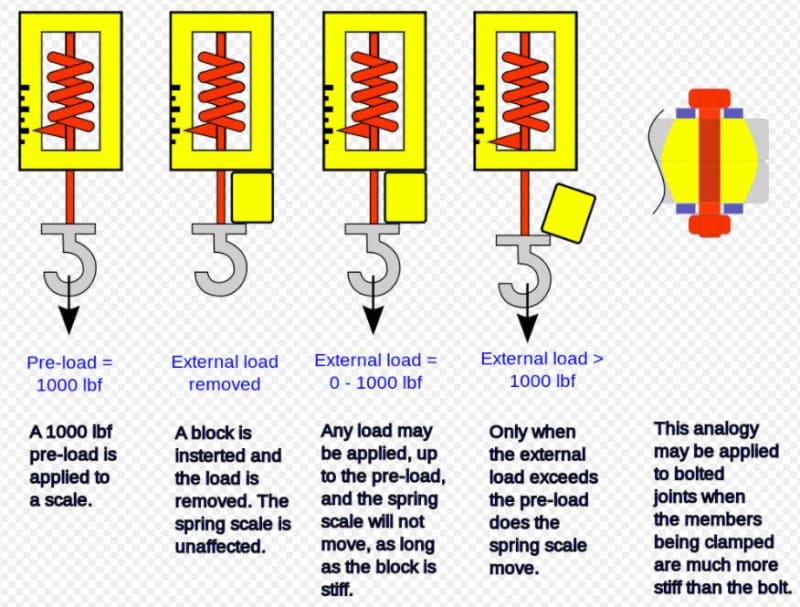
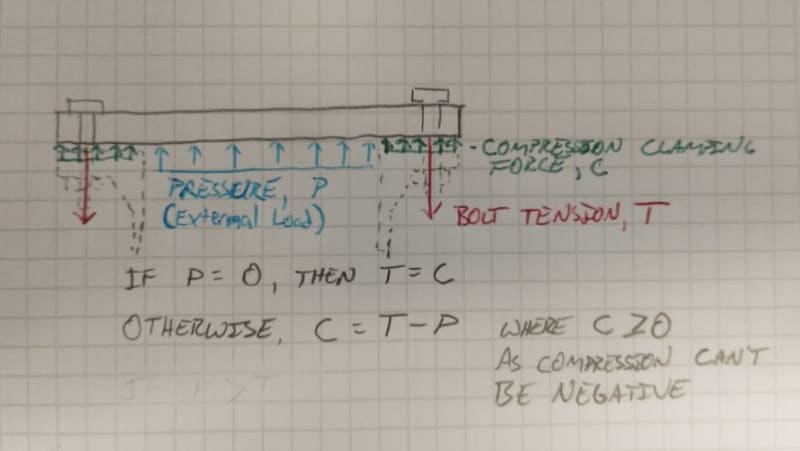
But... the assembly is not pressurized when I'm tightening those bolts. By just tightening them, I've already used up 92% of the bolts' reserve, not much left for when I will actually pressurize it.

If i will now calculate how much pressure this assembly can take after tightening the bolts, then I can only use the reserve left in the bolts (8 percent to yield strength) as in my calculation? That's not much...

Or lets give you another really simple example just to illustrate the point I'm trying to make here:
Lets say you have an M6 eye bolt, you insert it through a hole in a rigid steel plate in the ceiling, and screw a nut on the other side. If the nut is not tightened, then you can hang 11.29 kN load on your eye bolt before it breaks, but after you've tightened the nut according to VDI2230, you can only hang 11.29 kN x 8% = 0.9 kN off it before it snaps!.

I'm kinda confused here. What am I missing? All the example calculations I have seen for pressurized flanges, lids, end caps on pressure vessels etc just use the full capacity of the bolts in their strength calculations. But how can I do that if I've already used up 9/10 of it???

Could I tighten the nuts to a lesser torque than specified? But wouldn't the flange then leak, and would the bolts rattle loose / become undone too easily?

Thanks for any feedback (or for proving me stupid, it that happens to be the case

J.

desertfox · Jan 8, 2021

Hi Nordic8

I think I see where you are confused, I think you are assuming that all the load when your vessel is pressurised is carried by the bolts and that is not correct.
When you tighten the end cap on the vessel you tension the bolts but at the same time, the end flange compresses slightly against the end of the vessel, now when you pressurise the vessel the load is actually shared by both the bolts and the mating flange, the flanges are trying to release the compressive stress they are under which in order to do so must absorb some of the load and the remainder of the load is shared be the bolts. See this link

Why bolt preload is important

I should of also said that the majority of the external load on a bolted joint is carried by the clamped members due to the fact that clamped members are usually much stiffer than the bolts.

“Do not worry about your problems with mathematics, I assure you mine are far greater.” Albert Einstein

goutam_freelance · Jan 8, 2021

You need to calculate bolt stress considering both preload and working load.

Now the yielding factor of safety is S_p/sigma_b, S_p is bolt proof stress.

dauwerda · Jan 8, 2021

Bolt preload is not additive to the external force applied.

desertfox said:
I think you are assuming that all the load when your vessel is pressurised is carried by the bolts and that is not correct.

I am going to have to disagree with this statement. The load is most definitely carried by the bolts, there is no other load path. However Preload of a bolt is an internal force and the application of an external force is not additive to that internal force.

The confusion lies in not considering the change in the internal forces of the joint. When you torque the bolts, you develop a tension, or preload, in the bolt by clamping the flanges together. This clamping force results in the flange and end cap pushing on each other with a force that is equal and opposite and is in direct relation to the tension in the bolt. So, your entire joint is in equilibrium but there are all sorts of internal stresses. Now, you apply pressure to the end cap, this results in the compression force between the flange end endcap decreasing by the same amount that your external pressure applies a force. See the picture below to see what I mean:

rb1957 · Jan 8, 2021

you 've got several responses saying the same (correct IMO) thing ... external load is not added to the preload. preload compresses the joint together and reacts the large proportion of the applied load. A simplistic bolt load diagram shows the load in the bolt is the preload until the applied load = preload when the joint gaps and all the load is now carried by the bolt. Thus the bolt is still good for it's rated load whatever the preload.

another day in paradise, or is paradise one day closer ?

desertfox · Jan 8, 2021

dauwerds

The bolts do not see all the external load that is not incorrect, the external load is shared between the clamped parts and the bolts and that’s what I have explained. If the bolt sees all the load the joint will be on the verge of separation.

dauwards said:
Now, you apply pressure to the end cap, this results in the compression force between the flange end endcap decreasing by the same amount that your external pressure applies a force.

the above statement by you is actually incorrect because the bolt stretches to accommodate a slight increase in tension as the compressive stresses are relieved between the clamped end cap and vessel, what you are implying the bolt sees no additional load due to the external force and that is incorect. its also a contradiction because you state the bolts see all the load.

dauwards said:
The load is most definitely carried by the bolts, there is no other load path

“Do not worry about your problems with mathematics, I assure you mine are far greater.” Albert Einstein

dauwerda · Jan 8, 2021

desertfox said:
If the bolt sees all the load the joint will be on the verge of separation.

That depends on how large the external load is. If it is less than the preload than there is still a clamping force (equal to the initial clamping force minus the external load). If the external load is equal to the preload, the clamping force is zero (i.e. on the verge of separation). If the external force is greater than the preload, then yes, the joint will absolutely separate.

Draw a free body diagram of the joint and show me how there is any situation where the bolts are not resisting the full pressure.

rb1957 · Jan 8, 2021

you guys realise you're both saying the same thing ?

when the joint is clamped together the external load is shared between the joint faces (compression) and the bolt
when the joint is gapped, all the eternal load is reacted by the bolt.

another day in paradise, or is paradise one day closer ?

desertfox · Jan 8, 2021

Hi rb1957

Well clearly dauwerda doesn't see it like that but now his post is misleading because in one post he is saying the bolts take all the load but in his text as quoted by dauwerda he states the whole external load is taken by the end cap and vessel releasing some compressive stress.

“Do not worry about your problems with mathematics, I assure you mine are far greater.” Albert Einstein

dauwerda · Jan 8, 2021

No rb1957, we are not saying the same thing. In fact, your first statement, "when the joint is clamped together the external load is shared between the joint faces (compression) and the bolt" is also incorrect.

The external load applied on the cap is only ever resisted by the bolt tension, there is no sharing this tension with the joint faces.
You could say that the tension in the bolt is resisted by both the external force and the clamping force. That is, as the external force is increased, the clamping force decreases so that the tension in the bolt remains constant.

dauwerda · Jan 8, 2021

We are clearly having some disconnect here.

desertfox said:
Well clearly dauwerda doesn't see it like that but now his post is misleading because in one post he is saying the bolts take all the load but in his text as quoted by dauwerda he states the whole external load is taken by the end cap

I am not trying to be misleading. The pressure is applied to the end cap. The reason the end cap doesn't blow away is that the bolts resist that force. The bolts transfer the full force of the external pressure that is applied to the endcap. This is true whether they are preloaded or not.

Again, I believe this is a very misleading statement:

desertfox said:
I think you are assuming that all the load when your vessel is pressurised is carried by the bolts and that is not correct.

I interpret that as somehow meaning there is some other mechanism in place (other than the bolts) that resists the load applied to the end cap. All of the load is absolutely carried by the bolts.

The confusion the OP had was that he/she was trying to add the tension force due to the pressure to the preload tension of the bolt. This is not the correct approach. Rather than being additive, The tension in the bolt remains the same, as the external load increases the clamping force between the parts decrease. The external force applied on the end cap is still however, only resisted by the bolts.

rb1957 · Jan 8, 2021

"You could say that the tension in the bolt is resisted by both the external force and the clamping force. That is, as the external force is increased, the clamping force decreases so that the tension in the bolt remains constant." ... that is exactly, exactly, what I am saying ... "the external load is shared between the joint faces (compression) and the bolt" Possibly my "(compression)" is clouding the statement ... external tension load will increase the bolt tension and reduce the joint compression; until the joint compression is zero (the joint is gapped) and all the external load is in the bolt.

another day in paradise, or is paradise one day closer ?

goutam_freelance · Jan 8, 2021

I think that we need to think about the problem conceptually. This is not simple static determinacy problem but a statically indeterminate problem where the displacement compatibility(flange faces move together as long as joint is tight) to be ensured.
Now we take initial position of flange faces as 0 after applying preload. Now due to external load a increase of length delta takes place in bolt. This is also the increase in thickness of flanges considered together(reduction in strain).

From the above it is apparent that external load P is shared between bolts and flanges.

Engineers, think what we have done to the environment !

https://www.linkedin.com/in/goutam-das-59743b30/

rb1957 · Jan 8, 2021

I'm off to the pub ...

another day in paradise, or is paradise one day closer ?

dauwerda · Jan 8, 2021

rb1957 said:
that is exactly, exactly, what I am saying

It's not though.

rb1957 said:
"the external load is shared between the joint faces (compression) and the bolt"

We all agree that the external load is the pressure that is on the end cap, correct?

The compression on the joint faces is due to an internal load (bolt pretension), it is not due to an external load (pressure in vessel).
Stating that the load is shared between the joint faces and the bolt is very misleading. The joint faces are not resisting the external load. The joint faces are resisting the internal load that is caused by the clamping force due to bolt pretension. As an external load is applied to the endcap, it is only resisted by the bolts (no sharing). However, as stated before, this results in the internal clamping force (caused by the bolts) to decrease.

rb1957 said:
external tension load will increase the bolt tension and reduce the joint compression;

No. The external tension load (again, this is the pressure on the end cap) will reduce the joint compression and the bolt tension will remain the same.

rb1957 said:
until the joint compression is zero (the joint is gapped) and all the external load is in the bolt.

Yes. Except that all of the external load was always in the bolt. The change is that there is no longer any load in the bolt due to the resistance of the clamped parts.

goutam_freelance · Jan 8, 2021

In which country pubs are open? Curious...

Engineers, think what we have done to the environment !

https://www.linkedin.com/in/goutam-das-59743b30/

desertfox · Jan 8, 2021

My absolute agreement with you rb1957

I stated this in my first post but it seems to have been ignored by dauwerda

desertfox said:
now when you pressurise the vessel the load is actually shared by both the bolts and the mating flange,

My reference to all the load being carried by the bolts was that the external load on the vessel due to the internal pressure plus the bolt preload was the total load in the bolt and that is not correct but I believe thats what the OP thinks.
example two plates 10mm thick clamped together with an M16 bolt and a bolt preload of 40KN which is then subject to a external load of 30KN what is the total tension in the bolt dauwerda?

No dauwerda the bolt tension won't remain the same.

dauwerda said:
The external tension load (again, this is the pressure on the end cap) will reduce the joint compression and the bolt tension will remain the same.

“Do not worry about your problems with mathematics, I assure you mine are far greater.” Albert Einstein

dauwerda · Jan 8, 2021

desertfox said:
example two plates 10mm thick clamped together with an M16 bolt and a bolt preload of 40KN which is then subject to a external load of 30KN what is the total tension in the bolt dauwerda?

The tension in the bolt is 40kN
You start with a tension in the bolt that is 40kN, this is resisted by the compression between the two faces of the joint, also equal to 40kN.
You apply an external load of 30kN. The bolt still has a tension force of 40kN, however to maintain equilibrium, this means the compression force between the faces of the plates is now only 10kN.

desertfox said:
No dauwerda the bolt tension won't remain the same.

Unless you disagree with my answer above, yes it does remain the same.

Please go back and look at the initial picture that I posted (actually, I'll repost it). For the OP's example the red spring is the bolt, the yellow box holding the spring scale is the flange and the block that is in inserted would be the endcap. The external load applied to the hook would be the pressure applied to the endcap.

As can be seen in that image, the external force is only resisted by the bolt tension. The the block or endcap does not magically stick to the flange without the bolt (this is what load sharing would imply). The clamping force is a function of both the bolt preload and the external load. i.e. the clamping force changes when the external load changes, but this does not mean that the flange faces "share" the external load with the bolt.

dauwerda · Jan 8, 2021

goutam_freelance said:
In which country pubs are open? Curious...

I could be wrong, but I believe rb1957 was referring to this forum,

https://www.eng-tips.com/threadminder.cfm?pid=1088

desertfox · Jan 8, 2021

yes dauwerda I disagree I will post shortly

“Do not worry about your problems with mathematics, I assure you mine are far greater.” Albert Einstein

Tek-Tips is the largest IT community on the Internet today!

Members share and learn making Tek-Tips Forums the best source of peer-reviewed technical information on the Internet!

Bolt load capacity after tightening 15

Mechanical

Mechanical

Mechanical

Structural

Aerospace

Mechanical

Structural

Aerospace

Mechanical

Structural

Structural

Aerospace

Mechanical

Aerospace

Structural

Mechanical

Mechanical

Structural

Structural

Mechanical

Similar threads

Log in

Part and Inventory Search

Sponsor