Finding coordinates of a point using two theodolites
Finding coordinates of a point using two theodolites
(OP)
Here is a topography problem that is currently stumping me.
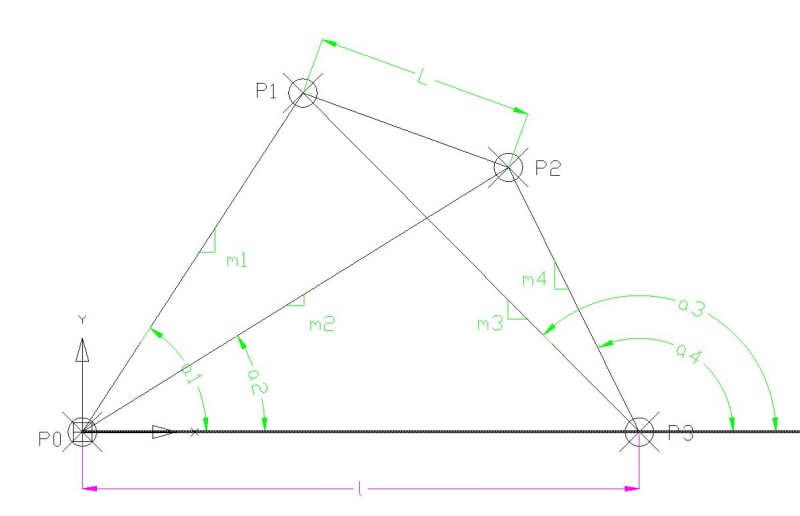
The problem statement simple:
Given:
Find:
The real life situation is that I have two theodolites at points P0 and P3.
I also have a length of steel bar with two points (P1 and P2) marked on it for which I know the precise spacing (L). I place this bar on the ground at a suitable but unknown distance from my two theodolites.
I colimate both theodolites to establish base angle 0 deg and proceed to measure all 4 horizontal angles a1 to a4 as measured from that baseline.
Precise colimation is important here to maintain accuracy.
By calculation, I then find l.
Once I found l, I'll be able to point both theodolites on any other point Px, read the two horizontal angles and figure 2D coordinates of Px by simple triangulation.
Some of you may suggest to simply measure the distance between my theos, but I dont want to do this. Lose to much accuracy.
The next step will be to figure out the 3D solution for this problem by adding in the vertical angle readings.
Ultimate goal is to figure out 3D coords of Px.
I am sure this is a problem that has been solved many times.
So this is what ive done so far:
Write the equations of all 4 lines in the usual form y=mx+b:
Y1=m1X1+0 (1)
Y1=m3X1+b3 (2)
Y2=m2X2+0 (3)
Y2=m4X4+b4 (4)
From (2) at X=0:
l= -b3/m3 (5)
From (4) at x=0:
l= -b4/m4 (6)
From (5) = (6):
b3/b4 = m3/m4 (7)
From (1) = (2):
(m1-m3)X1 = b3 (8)
From (3) = (4):
(m2-m4)X2 = b4 (9)
Plug (8) and (9) in (7):
X1/X2 = [m3(m2-m1)] / [m4(m1-m3)] (10)
So now down to 1 equation (10) and 2 unknowns (X1, X2).
Try introducing L:
L2 = (X2-X1)2 + (Y2-Y1)2 (11)
Now have 2 equations: (10) and (11), 4 unknowns: X1, Y1, X2, Y2.
So adding in a bit of trig:
X1 = l1 Cos(a1) (12)
Y1 = l1 Sin(a1) (13)
l-X2 = l4 Cos(a3) (14)
Y2 = l4 Sin (a3) (15)
Now have 6 equations: (10) to (15), 7 unknowns: X1, Y1, X2, Y2, l1, l4 and l.
Still short 1 equation to be able to solve...
I've looked at introducing scalene triangle rules (Law of cosines, Law of sines) but that just seems to add more and more unknowns (lengths).
I believe I am missing an obvious equation to tie everything together.
Any suggestions anyone?
Thanks and Happy Holidays!
The problem statement simple:
Given:
Angles a1 to a4 (or slopes m1 to m4, same thing)
Distance L
Find:
Distance l
The real life situation is that I have two theodolites at points P0 and P3.
I also have a length of steel bar with two points (P1 and P2) marked on it for which I know the precise spacing (L). I place this bar on the ground at a suitable but unknown distance from my two theodolites.
I colimate both theodolites to establish base angle 0 deg and proceed to measure all 4 horizontal angles a1 to a4 as measured from that baseline.
Precise colimation is important here to maintain accuracy.
By calculation, I then find l.
Once I found l, I'll be able to point both theodolites on any other point Px, read the two horizontal angles and figure 2D coordinates of Px by simple triangulation.
Some of you may suggest to simply measure the distance between my theos, but I dont want to do this. Lose to much accuracy.
The next step will be to figure out the 3D solution for this problem by adding in the vertical angle readings.
Ultimate goal is to figure out 3D coords of Px.
I am sure this is a problem that has been solved many times.
So this is what ive done so far:
Write the equations of all 4 lines in the usual form y=mx+b:
Y1=m1X1+0 (1)
Y1=m3X1+b3 (2)
Y2=m2X2+0 (3)
Y2=m4X4+b4 (4)
From (2) at X=0:
l= -b3/m3 (5)
From (4) at x=0:
l= -b4/m4 (6)
From (5) = (6):
b3/b4 = m3/m4 (7)
From (1) = (2):
(m1-m3)X1 = b3 (8)
From (3) = (4):
(m2-m4)X2 = b4 (9)
Plug (8) and (9) in (7):
X1/X2 = [m3(m2-m1)] / [m4(m1-m3)] (10)
So now down to 1 equation (10) and 2 unknowns (X1, X2).
Try introducing L:
L2 = (X2-X1)2 + (Y2-Y1)2 (11)
Now have 2 equations: (10) and (11), 4 unknowns: X1, Y1, X2, Y2.
So adding in a bit of trig:
X1 = l1 Cos(a1) (12)
Y1 = l1 Sin(a1) (13)
l-X2 = l4 Cos(a3) (14)
Y2 = l4 Sin (a3) (15)
Now have 6 equations: (10) to (15), 7 unknowns: X1, Y1, X2, Y2, l1, l4 and l.
Still short 1 equation to be able to solve...
I've looked at introducing scalene triangle rules (Law of cosines, Law of sines) but that just seems to add more and more unknowns (lengths).
I believe I am missing an obvious equation to tie everything together.
Any suggestions anyone?
Thanks and Happy Holidays!
Talk To Other Members
RE: Finding coordinates of a point using two theodolites
For everyone's benefit, here it the complete solution:
A bit of trig:
(Note: Angles a3 and a4 below are the complementary angles to those shown on the sketch above)
X1 = l1 cos (a1)
Y1 = l1 sin (a1)
X2 = l2 cos (a2)
Y2 = l2 sin (a2)
Find angles:
Angle P0P1P3 : Call it b1 = 180 - a1 - a4
Angle P0P2P3 : Call it b2 = 180 - a2 - a3
From Law of Sines:
l / sin (b1) = l1 / sin (a4) ==> l / l1 = sin (b1) / sin (a4) = K1 ==> l1 = l / K1
l / sin (b2) = l2 / sin (a3) ==> l / l2 = sin (b2) / sin (a3) = K2 ==> l2 = l / K2
Combine Law of Sines and trig:
X1 = l/K1 * cos(a1) ==> Say F1 = cos(a1)/K1 ==> X1= l * F1
Y1 = l/K1 * sin(a1) ==> similarly Y1 = l * F2
X2 = l/K2 * cos(a2) ==> similarly X2 = l * F3
Y2 = l/K2 * sin(a2) ==> similarly Y2 = l * F4
A bit of Pythagora's Theorem with X1, X2, Y1 and Y2:
L2 = (X2 - X1)2 + (Y2-Y1)2
Substitute and rearrange:
L2 = l2 (F12 + F22 + F32 + F42) - l (F1F2+F3F4)
Say:
C1 = (F12 + F22 + F32 + F42)
C2 = (F1F2+F3F4)
Then solution for l is this quadratic equation:
C1 l2 - C2 l - L2 = 0
Now I need to step this up a notch by adding a Z dimension to the problem.
Given:
Horizontal angles a1 to a4
Vertical Angles b1 to b4
Vertical angle between P0P3 and X axis
And distance L (length of P1P2)
Find:
Distance l (length P0P3)
I'll get cracking on that.
Will likely follow same logic as for 2D solution.
Will welcome anybody who wants to pitch in any additional suggestions.
Solution to that will allow me to establish 3D coordinates of any point is space using two theodolites.
RE: Finding coordinates of a point using two theodolites
I=I1 + I4 +x2 - x1
Not sure if it’s an independent equation.
L is given, but are you certain it’s a 2d distance, that bar is level?
RE: Finding coordinates of a point using two theodolites
Yes, I have put some thoughts about the levelness of the bar.
Being that this is being done indoors and that the bar is set on the floor I consider it to be level enough.
Thanks,
RE: Finding coordinates of a point using two theodolites
TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! https://www.youtube.com/watch?v=BKorP55Aqvg
FAQ731-376: Eng-Tips.com Forum Policies forum1529: Translation Assistance for Engineers Entire Forum list http://www.eng-tips.com/forumlist.cfm
RE: Finding coordinates of a point using two theodolites
Especially with today's laser scanning equipment, range finders and all other equipment.
However, if you want to scan a relatively complexe geometry, dont need too dense a point cloud and all you have is a pair of vintage T2s and time on your hands, that's the way to go!
The solution to the 2D calculation above was just a stepping stone to what I really need which is a solution to the 3D equivalent of the above problem.
RE: Finding coordinates of a point using two theodolites
TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! https://www.youtube.com/watch?v=BKorP55Aqvg
FAQ731-376: Eng-Tips.com Forum Policies forum1529: Translation Assistance for Engineers Entire Forum list http://www.eng-tips.com/forumlist.cfm
RE: Finding coordinates of a point using two theodolites
However, being at equal heights, I firmly believe, is of no importance at all in both the 2D and 3D scenarios.
In 2D, you would be shooting the points and considering only the horizontal angle readings from the theodilites and all resulting distances would be in the horizontal plane only. Picture observing the scene from above. Height and vertical angles would be invisible to you. This also highlights the importance of having that bar flat when establishing the coord system since you are using the actual distance between the points on that bar. If its not flat, there would be no way of easily knowing g the horizontal distance between them.
In 3D, (once i figure out the equations to establish the coor system), you'll be considering the vertical angles from each theo and you will also consider the vertical angle between the two theodolites when doing the math to establish the coord system.
The one important step in both scenarios will be the proper collimation of the theodolites. This has to be correctly done in order to precisely establish the base 0-deg horizontal angle from which all other horizontal angles are measured.
Pretty certain my logic is right here. Let me know if you think im wrong.
RE: Finding coordinates of a point using two theodolites
Rather than think climate change and the corona virus as science, think of it as the wrath of God. Feel any better?
-Dik
RE: Finding coordinates of a point using two theodolites
https://tmackinnon.com/surveying-from-an-unknown-p...