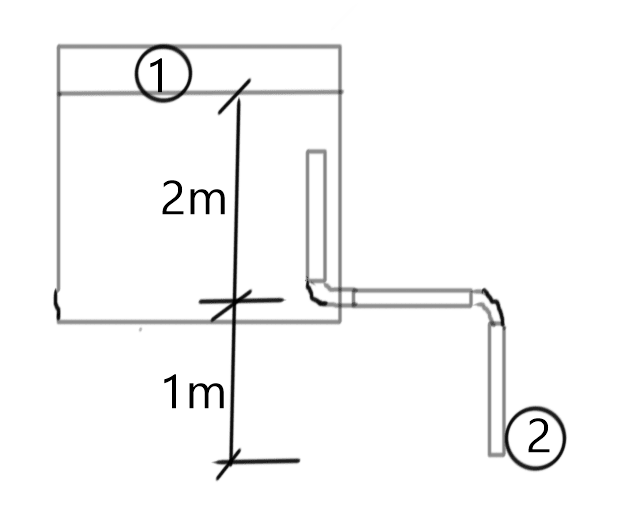
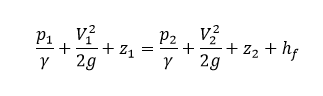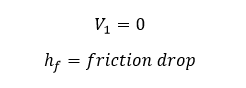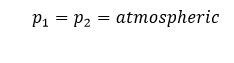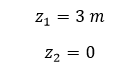So I know this is something that's been asked before, but I haven't seen any real considerations for the pipe that a tank will drain into.
I have a 2.5" drain line out of the side of a tank, so using Q = a*Cd*(2gh)^0.5;
a = 5.45 in^2 = 0.00352 m^2
Cd = borda outlet = 0.51
h = 2m
So, Q = 0.0112 m^3/s = 178 gpm max flow rate from the tank.
Now, my understanding is that this is free flow out of the tank outlet as if it were open to the atmosphere. But lets say I have the equivalent of 50' of straight 2.5" pipe draining into a sump tank that is another meter below the drain outlet. How does the height difference between outlet and sump tank and the pipe friction between the tanks get included in the calculations? Is it as easy as adding the 1m height difference and subtract the head loss from the pipe to the H value? Does it need to be 2 different calculations?
Thanks.
I have a 2.5" drain line out of the side of a tank, so using Q = a*Cd*(2gh)^0.5;
a = 5.45 in^2 = 0.00352 m^2
Cd = borda outlet = 0.51
h = 2m
So, Q = 0.0112 m^3/s = 178 gpm max flow rate from the tank.
Now, my understanding is that this is free flow out of the tank outlet as if it were open to the atmosphere. But lets say I have the equivalent of 50' of straight 2.5" pipe draining into a sump tank that is another meter below the drain outlet. How does the height difference between outlet and sump tank and the pipe friction between the tanks get included in the calculations? Is it as easy as adding the 1m height difference and subtract the head loss from the pipe to the H value? Does it need to be 2 different calculations?
Thanks.

![[upsidedown] [upsidedown] [upsidedown]](/data/assets/smilies/upsidedown.gif)