Saedhalteh
Civil/Environmental
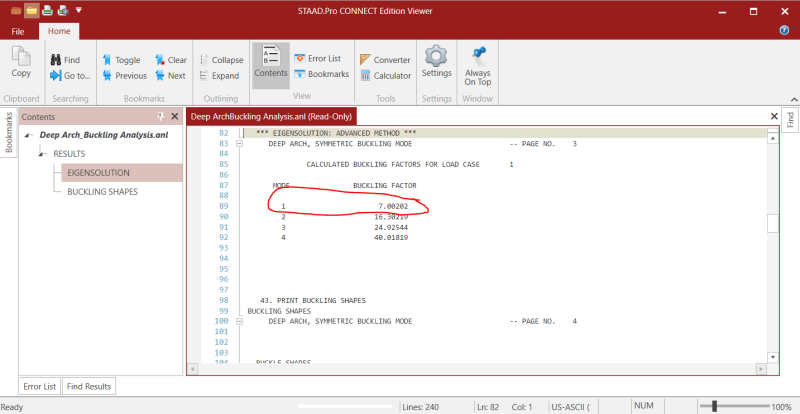
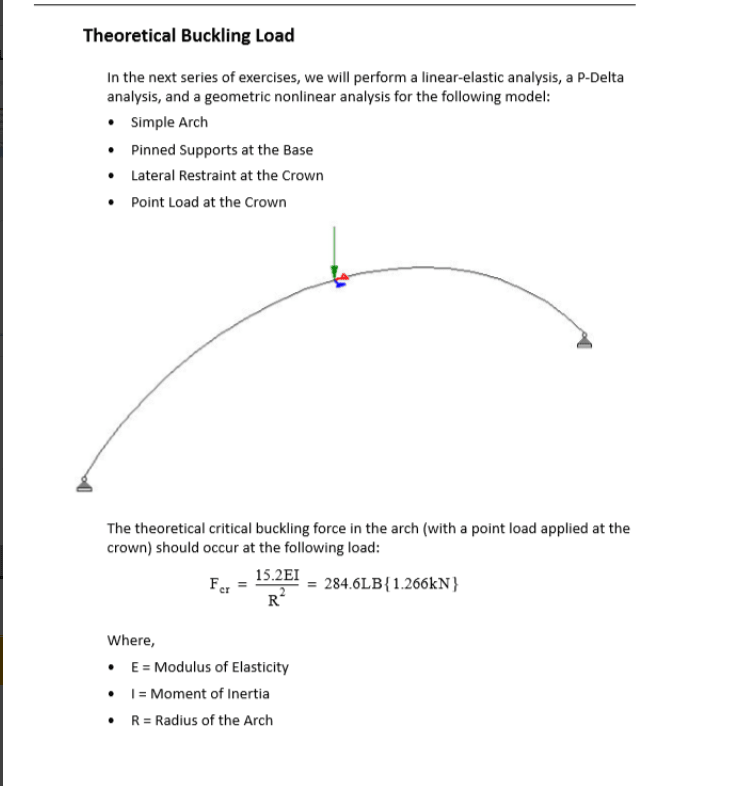
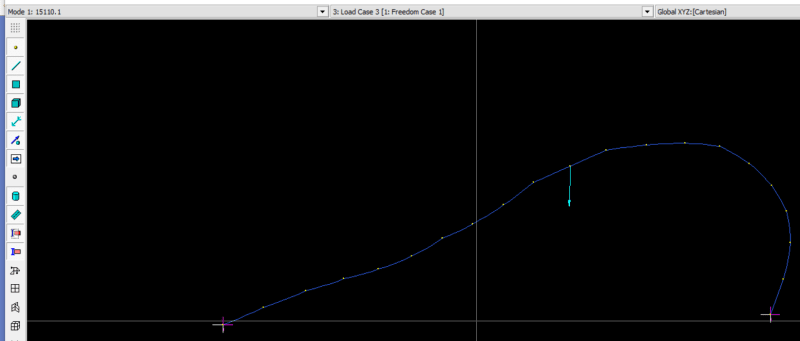
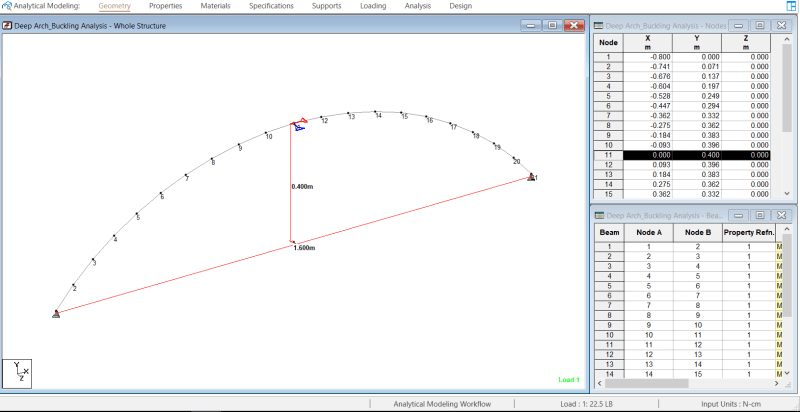
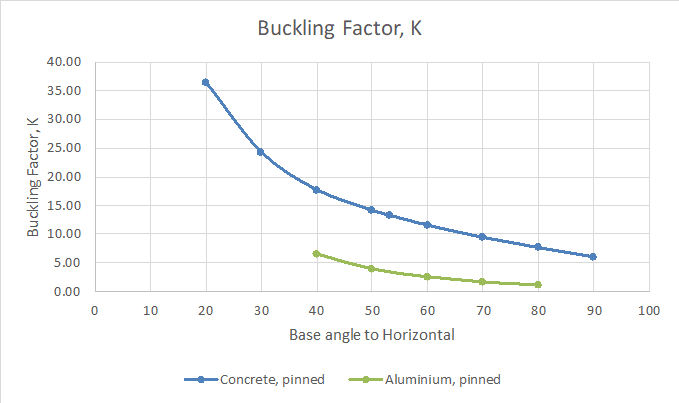
There is a ptoblem that I tried to solve with different types of analyisis Using STAAD software ,for the arched beam that I am trying to analyze the theoretical buckling load was 284 lb , using the linear elastic analysis it didnt show any failure . P delta analysis indicated failure at load much higher than 284 , non linear analysis gave the most accurate result with buckling load around 280 , but using the buckling analysis it showd me that the buckle should occur at 157.5 , I searched and understand the diffrences between the linear, p-delta and non linear analysis. My question is why the buckling analysis gave results that differs alot from the non linear analysis ? Can someone help me with that.