Strain Compatibility of Unbonded PT 2

Celt83,

Correct, there is no strain compatibility.

The balance moment = P.e + Msec.

Msec is part of the applied moment.

So the resistance moment from PT = P.e

But as the beam deflects the tendon elongates slightly so P is increased. The code gives a very approximate formula for this increase. So P is not the prestress force after losses, it is increased slightly due to flexure of the member.

Rapt:
Thank you for the reply. I think what I struggle with is if the unbonded tendon is in a greased duct and the cross section under goes a curvature change I picture the tendon free to slip and elongate but the additional axial force from that elongation only gets applied to the cross section at the anchorage points and at an infinitesimal section within the span the action of the tendon on the cross section is applying additional vertical force like straightening a rope the force application point is at my hands and the action of the rope is to lift up. Maybe the rope analogy is wrong which may be my first problem.

Edit:
My initial rope analogy really describes the initial PT load application. For the ultimate load state the analogy I think of is if I am holding the rope tight and someone pushes down on it my hands experience more force but their finger experiences a vertical resisting force.

Edit2:
Thinking a bit more with increase elongation there is added overall compression due to the anchorage which would yield a higher neutral axis location and a larger moment arm between the bonded mild reinf and the concrete compression block..so ultimate cross section strength should be higher than if just the mild steel was considered.

Edit3:
Some more confusion on my end when computing Phi*Mn for the cross section it is compared to Mu from the applied loads + the hyperstatic moments caused by the PT, I think I'm instinctively trying to compare Phi*Mn to the net cross section bending moment which would have the pt force effect accounted for already.

Open Source Structural Applications:

Celt83,

Yes, all weird concepts. Might be why most of the world does bonded PT! The Australian building code does not even allow unbonded PT in buildings except slab on grade.

Note sure what you mean by edit3!

Rapt:
think I'm starting to get it...my edit 3 I believe has whats been giving me struggle when I only try to mentally think of the moment capcity vs actually write it out.

Reality is phi*Mn >= Mu,factored applied loads + M,hyperstatic but in my head I want to do phi*Mn >= Mu,factored applied loads + M,hyperstatic - M,balance. If I did what's in my head vs what I write then my check on the moment would be double dipping on the balance force.



Edit: In the ultimate force diagram there is no F,pt compressive force at the cross section centroid because the P/A compressive stress is already accounted for in the parabolic stress distribution since we've essentially continued along the load history from the service stress-diagram and pumped the strain up to the ultimate strain.

The F,pt tensile force can be directly used even though its in a greased duck for the same reason you can use both chord forces in a truss section cut between panel points, in other words simple statics.

Open Source Structural Applications:

Celt83

Firstly, You are getting mixed up with your Balanced Moment and Msec. Balanced includes Msec (P.e + Msec).

The other problem you are having is thinking of the service case in its simplified working stress methodology while you are looking at ultimate as strain compatibility.
In the simplified service case, if you do as you do at ultimate and include Msec in the applied stress and treat the PT effect as P at an eccentricity of e, then you will get exactly the same result but the logic is the same as for ultimate.

If you look at service as strain compatibility assuming concrete has tensile strength and a linear stress/strain for concrete (triangular diagram) then the methodology is the same as for ultimate.

The difference for the PT at ultimate is that e increases as the neutral axis rises and P increases as the tendon extends due to flexure. So you have (P + DeltaP) . (e + deltae) as the effect of the prestress.

It is even easier if you think of the concrete as a parabolic stress/strain curve as it is then an easy progression from service to ultimate. The rectangular stress block complicates it by making ultimate look different to service.

Rapt:
Think we are on the same page now with exception that I am/was using the wrong terminology.

What you suggest in your last paragraph made things much more clear I essentially just kept stepping thru the load history and drawing new strain and stress diagrams considering a parabolic stress profile for the concrete.

I appreciate you taking the time to run thru this.

Open Source Structural Applications:

Celt83 said:

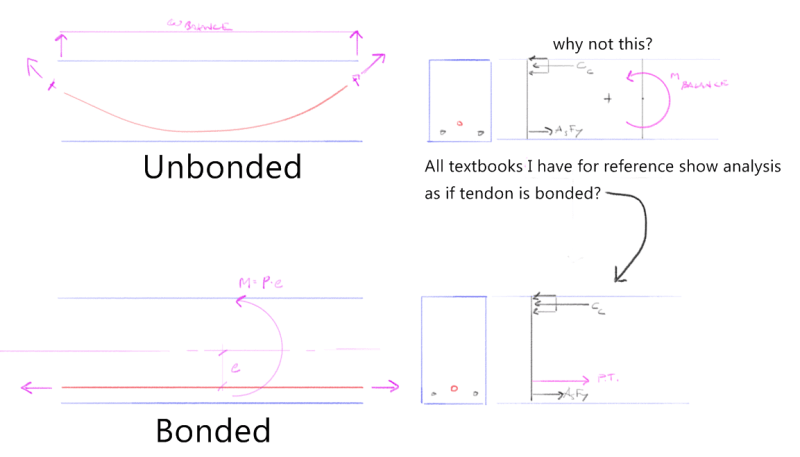
This is likely a dumb question but it has puzzled me a bit, all the reference texts I've seen on the subject show the tendon force applied at the tendon elevation in the cross section for the strain compatibility analysis. What I have trouble wrapping my head around is that in an unbonded system there is no bond so shouldn't the strain analysis only consider the stress block, steel, and the balance moment at the cross section in lieu of the PT force * distance to the neutral axis?

Click to expand...

Celt83 said:

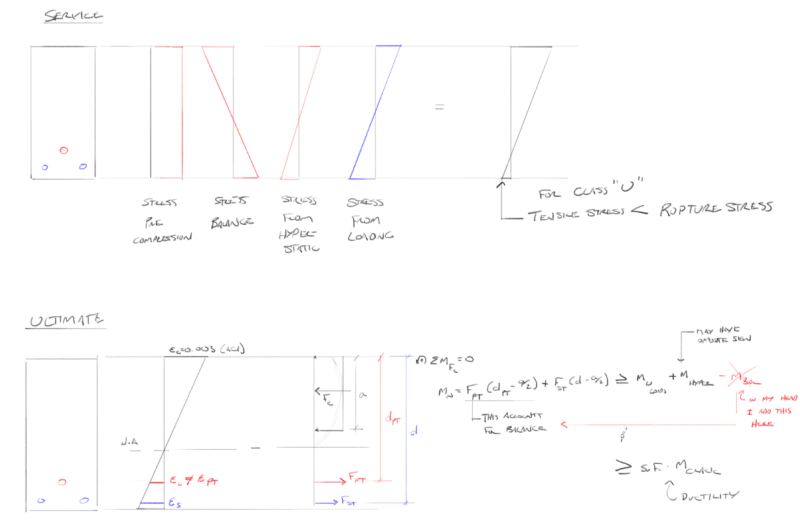
Reality is phi*Mn >= Mu,factored applied loads + M,hyperstatic but in my head I want to do phi*Mn >= Mu,factored applied loads + M,hyperstatic - M,balance. If I did what's in my head vs what I write then my check on the moment would be double dipping on the balance force.

Click to expand...

It sounds as though you've got this sorted now, probably from several angles. That said, I believe that I went through almost the exact same pain in a previous thread where rapt's input was instrumental in helping me get things sorted out: Link. I thought that you might benefit from hearing the story told from my perspective and from examining some of the sketches that I developed to help me get my ship righted on this.

OLD KOOTK QUESTION:

In the ultimate flexure calculations, you always see the PT force placed at the level of the PT. How did it get there given that it started off at the end anchorage elevation and, in unbonded PT, there is no mechanism for the transfer of "bond stress" between the tendons and the surrounding concrete? No bond equals no strain compatibility, right?

NEW KOOTK UNDERSTANDING:

In draped PT beams, flexural resistance can/must be considered to be coming from two, independent but related sources:

1) The effect of the axial pre-stress acting alone and reducing cross section demand for tensile reinforcing.

2) The balancing load effect from tendon curvature effectively acting as a transverse loading on the concrete member to counteract external loads.

It is true that the balancing load can only be counted once, and I've stumbled on that myself in the past. However, it is also true that the balancing load effect is an integral part of the flexural resistance in a post-tensioned beam with drape.

The big takeaway for me considering the original question (read it again now for good measure please):

The applied PT force really has not moved from the elevation at which it originated at the anchorages. For flexural analysis, the unbonded PT force can be placed at the level of the tendons at any cross section because what is actually being represented is the summation of effects #1 & #2, described above. The balancing force stresses are essentially replaced by an equivalent, faux eccentricity to the original anchorage forces. And the net effect is just as rapt has described: P x e.

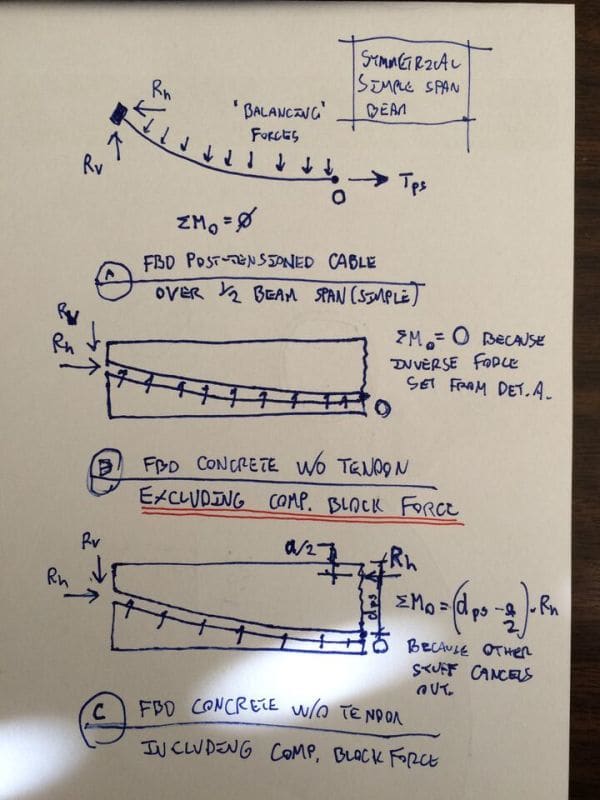
The first sketch below is my examination of the situation considering the tendons and the concrete as separate members, each acting upon the other appropriately. For some reason, I find that presentation a great help to my understanding.

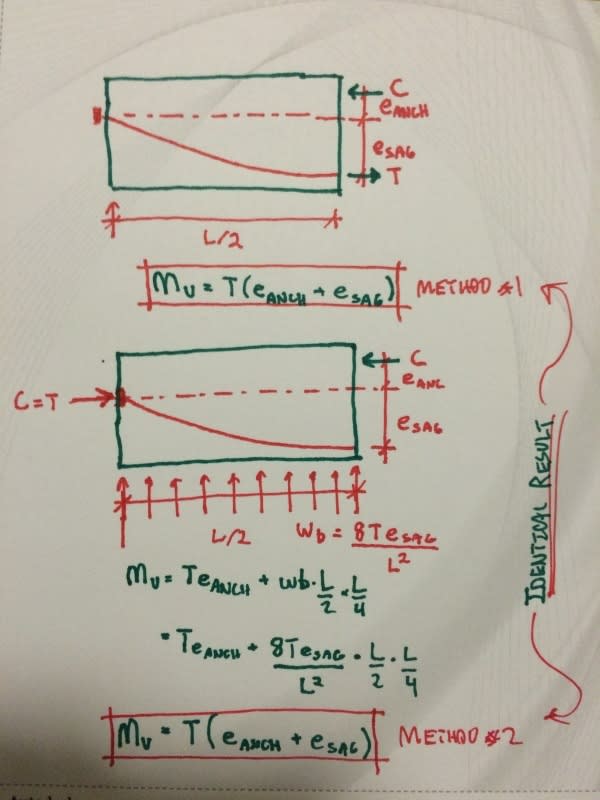
The second sketch is me using two different methods to determine flexural capacity, proving that both are valid and just different sides of the same coin:

A) Conventional P x e where the balancing load effect is buried in the "e" value.

B) An alternate formulation where the balancing load effect is considered explicitly.

I've got my fingers crossed hoping that I've added something meaningful to the conversation here for you. Otherwise, I'll have wasted a good chunk of football Sunday for nothing! Ah well, all investments are risks.

Note that most of what I've described and sketched is for simple span beams. Things get a bit more complex when secondary effects associated with continuity etc are considered. I've done things as I have not because I don't recognize that complexity but, rather, because the added complexity tends to obfuscate the truth of the points that I've tried to make.

Kootk:

Thanks for the response...reading thru your link sounds like we had basically the same hang up. You articulated it much better.

For me it boiled down to two fundemental things:
1. P*e is accounted for in the capacity so should never be included in the load side of the phi*Mn vs Mu check. Where P and e are as Rapt note larger due to the change in the cross section curvature increasing the tendon elongation and the neutral axis shift increasing the e.

2. Unbonded tendons are NOT cable structures.

Open Source Structural Applications:

Because I like to beat a dead horse has anyone looked into or done strut-and-tie modeling with unbonded draped post-tension tendons?

Edit:
Found this article on ACI there is a small section on unbonded tendons.

_ said:

Title: Strut-and-Tie Model for Externally Prestressed Concrete Beams

Author(s): K. H. Tan and A. E. Naaman

Publication: Structural Journal

Volume: 90

Issue: 6

Appears on pages(s): 683-691

Keywords: flexural strength; prestressed concrete; prestressing; shear stress; strength; strut-tie model; trusses; Design

Date: 11/1/1993

Click to expand...

Open Source Structural Applications:

@Celt: did you get a copy of that paper? I'm curious to know if there's any great stuff in there. This paper has some good stuff on STM for prestressed concrete although not for unbonded post tensioning specifically: Link

I think that the nature of PT is such that you're usually dealing with very slender elements for which STM tends to be less applicable than it is in general. Lots of Bernoulli region.
Obviously, there are all manner of STM applications surrounding local effects like anchorage detailing etc.

I was able to grab a copy via our office ACI membership while a good read it didn't really offer much from a practical standpoint.

The PDF in your link is much more informative....Thank you for sharing.

Open Source Structural Applications: