Mechanicslearner
Structural
Hello,
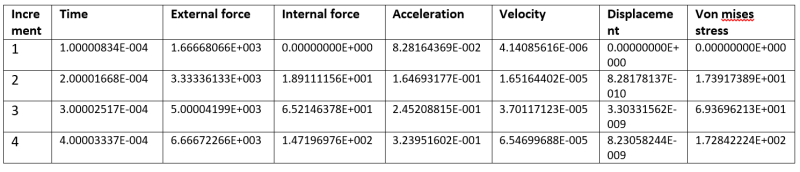
I am experimenting with non linear cantilever beam with axial point load at tip where stress levels decrease after reaching plasticity. You can see as follows
Yield stress------------- plastic strain
210000000------------- 0
232300000------------- 0.00884475
255000000------------- 0.01858908
278100000------------- 0.02823539
260000000------------- 0.03798338
241500000------------- 0.04764082
212000000------------- 0.05725989
246100000------------- 0.06648743
291600000------------- 0.07557343
327000000------------- 0.08462176
363000000------------- 0.0935831
399600000------------- 0.10245897
I know that if we use true stress and true strain , stress wont decrease that much but I am doing this just to learn how explicit works
in abaqus, I tried in implicit and abaqus standard where it gives error when stress levels try to decrease. Explicit worked great, where it gives little fluctuation curve when I apply very small load for each time step and vice versa (large fluctuations when load applied in small time).
So the question is how explicit calculates stress fluctuations
TIME IN
SECONDS------------- FORCE IN NEWTONS------------- STRESS IN N/M^2------------- PLASTIC STRAIN------------- MAX DISPLCAEMENT
0.------------- 0. ------------- 0. ------------- 0.------------- 0.
200.007E-03------------- 6.80023E+06------------- 13.622E+06 ------------- 0.------------- 648.472E-06
400.002E-03 ------------- 13.6001E+06 ------------- 27.1997E+06------------- 0.------------- 1.29395E-03
600.007E-03 ------------- 20.4002E+06------------- 40.8579E+06 ------------- 0.------------- 1.94486E-03
800.003E-03 ------------- 27.2001E+06------------- 54.3996E+06 ------------- 0.------------- 2.5888E-03
1.00001------------- 34.0002E+06------------- 68.07E+06 ------------- 0.------------- 3.24075E-03
1.2 ------------- 40.8001E+06------------- 81.5996E+06 ------------- 0.------------- 3.88445E-03
1.40001 ------------- 47.6002E+06 ------------- 95.261E+06 ------------- 0.------------- 4.5362E-03
1.6 ------------- 54.4001E+06------------- 108.8E+06 ------------- 0.------------- 5.18074E-03
1.80001 ------------- 61.2003E+06 ------------- 122.44E+06 ------------- 0.------------- 5.83151E-03
2. ------------- 68.0001E+06------------- 136.E+06 ------------- 0.------------- 6.47742E-03
2.2 ------------- 74.8001E+06------------- 149.625E+06 ------------- 0.------------- 7.127E-03
2.4 ------------- 81.6002E+06------------- 163.238E+06 ------------- 0.------------- 7.77555E-03
2.60001 ------------- 88.4002E+06------------- 176.803E+06 ------------- 0.------------- 8.42251E-03
2.80001 ------------- 95.2002E+06 ------------- 190.4E+06 ------------- 0.------------- 9.06965E-03
3.00001 ------------- 102.E+06 ------------- 204.E+06 ------------- 0.------------- 9.71818E-03
3.20001 ------------- 103.943E+06 ------------- 207.97E+06 ------------- 0.------------- 9.90617E-03
3.40001------------- 105.886E+06 ------------- 211.768E+06 ------------- 0.0007012------------- 16.4519E-03
3.6 ------------- 107.829E+06 ------------- 215.663E+06 ------------- 0.002246 ------------- 32.7624E-03
3.8 ------------- 109.771E+06 ------------- 219.774E+06 ------------- 0.003877 ------------- 48.9672E-03
4. ------------- 111.714E+06 ------------- 223.426E+06 ------------- 0.005325 ------------- 64.0021E-03
4.2 ------------- 113.657E+06 ------------- 227.311E+06------------- 0.006866 ------------- 79.2692E-03
4.40001 ------------- 115.6E+06 ------------- 231.197E+06------------- 0.008422 ------------- 95.2867E-03
4.6 ------------- 117.543E+06 ------------- 235.213E+06 ------------- 0.01012 ------------- 112.795E-03
4.8 ------------- 119.486E+06 ------------- 239.044E+06 ------------- 0.01175------------- 129.487E-03
5.00001 ------------- 121.429E+06 ------------- 242.854E+06 ------------- 0.01338------------- 145.941E-03
5.2 ------------- 123.371E+06 ------------- 246.741E+06------------- 0.01504------------- 163.372E-03
5.4 ------------- 125.314E+06------------- 250.732E+06 ------------- 0.01675 ------------- 180.792E-03
5.60001 ------------- 127.257E+06------------- 254.512E+06------------- 0.01835 ------------- 197.395E-03
5.8 ------------- 129.2E+06 ------------- 258.397E+06 ------------- 0.02000------------- 214.264E-03
6. ------------- 131.143E+06 ------------- 262.302E+06 ------------- 0.02164------------- 231.331E-03
6.20001 ------------- 133.086E+06------------- 266.199E+06 ------------- 0.02327------------- 248.149E-03
6.40001 ------------- 135.029E+06 ------------- 270.054E+06 ------------- 0.02495 ------------- 265.467E-03
6.60001 ------------- 136.971E+06 ------------- 274.E+06 ------------- 0.02700 ------------- 286.744E-03
6.8 ------------- 138.914E+06------------- 318.392E+06 ------------- 0.08671------------- 613.639E-03
7. ------------- 140.857E+06 ------------- 282.372E+06 ------------- 0.1006------------- 989.896E-03
7.20001 ------------- 142.8E+06 ------------- 341.619E+06 ------------- 0.1006------------- 992.474E-03
7.4 ------------- 144.743E+06------------- 289.048E+06 ------------- 0.1006 ------------- 989.228E-03
7.6 ------------- 146.686E+06 ------------- 300.987E+06 ------------- 0.1006 ------------- 991.31E-03
7.80001 ------------- 148.629E+06------------- 328.723E+06 ------------- 0.1006------------- 992.341E-03
8.00001------------- 150.572E+06 ------------- 300.798E+06 ------------- 0.1006------------- 989.983E-03
8.2 ------------- 152.514E+06------------- 304.804E+06 ------------- 0.1006------------- 990.702E-03
8.40001 ------------- 154.457E+06------------- 313.286E+06 ------------- 0.1006------------- 992.008E-03
8.6 ------------- 156.4E+06 ------------- 342.808E+06 ------------- 0.1006------------- 993.072E-03
8.80001 ------------- 158.343E+06 ------------- 349.E+06 ------------- 0.1006------------- 993.362E-03
9. ------------- 160.286E+06 ------------- 329.6E+06 ------------- 0.1006------------- 993.183E-03
9.20001 ------------- 162.229E+06------------- 324.321E+06------------- 0.1006------------- 993.244E-03
9.4 ------------- 164.171E+06 ------------- 328.262E+06 ------------- 0.1006------------- 994.491E-03
9.60001 ------------- 166.114E+06 ------------- 332.198E+06 ------------- 0.1006------------- 996.326E-03
9.8 ------------- 168.057E+06 ------------- 336.127E+06 ------------- 0.1006 ------------- 998.583E-03
10. ------------- 170.E+06 ------------- 340.005E+06 ------------- 0.1006 ------------- 1.00211
as you can see stress peaks at 6.8 second and decrease after that. May I know how abaqus explicit reached that value? I heard explicit does not do iteration and it calculates later time from current step. Unknown values are obtained from information already known.
I am experimenting with non linear cantilever beam with axial point load at tip where stress levels decrease after reaching plasticity. You can see as follows
Yield stress------------- plastic strain
210000000------------- 0
232300000------------- 0.00884475
255000000------------- 0.01858908
278100000------------- 0.02823539
260000000------------- 0.03798338
241500000------------- 0.04764082
212000000------------- 0.05725989
246100000------------- 0.06648743
291600000------------- 0.07557343
327000000------------- 0.08462176
363000000------------- 0.0935831
399600000------------- 0.10245897
I know that if we use true stress and true strain , stress wont decrease that much but I am doing this just to learn how explicit works
in abaqus, I tried in implicit and abaqus standard where it gives error when stress levels try to decrease. Explicit worked great, where it gives little fluctuation curve when I apply very small load for each time step and vice versa (large fluctuations when load applied in small time).
So the question is how explicit calculates stress fluctuations
TIME IN
SECONDS------------- FORCE IN NEWTONS------------- STRESS IN N/M^2------------- PLASTIC STRAIN------------- MAX DISPLCAEMENT
0.------------- 0. ------------- 0. ------------- 0.------------- 0.
200.007E-03------------- 6.80023E+06------------- 13.622E+06 ------------- 0.------------- 648.472E-06
400.002E-03 ------------- 13.6001E+06 ------------- 27.1997E+06------------- 0.------------- 1.29395E-03
600.007E-03 ------------- 20.4002E+06------------- 40.8579E+06 ------------- 0.------------- 1.94486E-03
800.003E-03 ------------- 27.2001E+06------------- 54.3996E+06 ------------- 0.------------- 2.5888E-03
1.00001------------- 34.0002E+06------------- 68.07E+06 ------------- 0.------------- 3.24075E-03
1.2 ------------- 40.8001E+06------------- 81.5996E+06 ------------- 0.------------- 3.88445E-03
1.40001 ------------- 47.6002E+06 ------------- 95.261E+06 ------------- 0.------------- 4.5362E-03
1.6 ------------- 54.4001E+06------------- 108.8E+06 ------------- 0.------------- 5.18074E-03
1.80001 ------------- 61.2003E+06 ------------- 122.44E+06 ------------- 0.------------- 5.83151E-03
2. ------------- 68.0001E+06------------- 136.E+06 ------------- 0.------------- 6.47742E-03
2.2 ------------- 74.8001E+06------------- 149.625E+06 ------------- 0.------------- 7.127E-03
2.4 ------------- 81.6002E+06------------- 163.238E+06 ------------- 0.------------- 7.77555E-03
2.60001 ------------- 88.4002E+06------------- 176.803E+06 ------------- 0.------------- 8.42251E-03
2.80001 ------------- 95.2002E+06 ------------- 190.4E+06 ------------- 0.------------- 9.06965E-03
3.00001 ------------- 102.E+06 ------------- 204.E+06 ------------- 0.------------- 9.71818E-03
3.20001 ------------- 103.943E+06 ------------- 207.97E+06 ------------- 0.------------- 9.90617E-03
3.40001------------- 105.886E+06 ------------- 211.768E+06 ------------- 0.0007012------------- 16.4519E-03
3.6 ------------- 107.829E+06 ------------- 215.663E+06 ------------- 0.002246 ------------- 32.7624E-03
3.8 ------------- 109.771E+06 ------------- 219.774E+06 ------------- 0.003877 ------------- 48.9672E-03
4. ------------- 111.714E+06 ------------- 223.426E+06 ------------- 0.005325 ------------- 64.0021E-03
4.2 ------------- 113.657E+06 ------------- 227.311E+06------------- 0.006866 ------------- 79.2692E-03
4.40001 ------------- 115.6E+06 ------------- 231.197E+06------------- 0.008422 ------------- 95.2867E-03
4.6 ------------- 117.543E+06 ------------- 235.213E+06 ------------- 0.01012 ------------- 112.795E-03
4.8 ------------- 119.486E+06 ------------- 239.044E+06 ------------- 0.01175------------- 129.487E-03
5.00001 ------------- 121.429E+06 ------------- 242.854E+06 ------------- 0.01338------------- 145.941E-03
5.2 ------------- 123.371E+06 ------------- 246.741E+06------------- 0.01504------------- 163.372E-03
5.4 ------------- 125.314E+06------------- 250.732E+06 ------------- 0.01675 ------------- 180.792E-03
5.60001 ------------- 127.257E+06------------- 254.512E+06------------- 0.01835 ------------- 197.395E-03
5.8 ------------- 129.2E+06 ------------- 258.397E+06 ------------- 0.02000------------- 214.264E-03
6. ------------- 131.143E+06 ------------- 262.302E+06 ------------- 0.02164------------- 231.331E-03
6.20001 ------------- 133.086E+06------------- 266.199E+06 ------------- 0.02327------------- 248.149E-03
6.40001 ------------- 135.029E+06 ------------- 270.054E+06 ------------- 0.02495 ------------- 265.467E-03
6.60001 ------------- 136.971E+06 ------------- 274.E+06 ------------- 0.02700 ------------- 286.744E-03
6.8 ------------- 138.914E+06------------- 318.392E+06 ------------- 0.08671------------- 613.639E-03
7. ------------- 140.857E+06 ------------- 282.372E+06 ------------- 0.1006------------- 989.896E-03
7.20001 ------------- 142.8E+06 ------------- 341.619E+06 ------------- 0.1006------------- 992.474E-03
7.4 ------------- 144.743E+06------------- 289.048E+06 ------------- 0.1006 ------------- 989.228E-03
7.6 ------------- 146.686E+06 ------------- 300.987E+06 ------------- 0.1006 ------------- 991.31E-03
7.80001 ------------- 148.629E+06------------- 328.723E+06 ------------- 0.1006------------- 992.341E-03
8.00001------------- 150.572E+06 ------------- 300.798E+06 ------------- 0.1006------------- 989.983E-03
8.2 ------------- 152.514E+06------------- 304.804E+06 ------------- 0.1006------------- 990.702E-03
8.40001 ------------- 154.457E+06------------- 313.286E+06 ------------- 0.1006------------- 992.008E-03
8.6 ------------- 156.4E+06 ------------- 342.808E+06 ------------- 0.1006------------- 993.072E-03
8.80001 ------------- 158.343E+06 ------------- 349.E+06 ------------- 0.1006------------- 993.362E-03
9. ------------- 160.286E+06 ------------- 329.6E+06 ------------- 0.1006------------- 993.183E-03
9.20001 ------------- 162.229E+06------------- 324.321E+06------------- 0.1006------------- 993.244E-03
9.4 ------------- 164.171E+06 ------------- 328.262E+06 ------------- 0.1006------------- 994.491E-03
9.60001 ------------- 166.114E+06 ------------- 332.198E+06 ------------- 0.1006------------- 996.326E-03
9.8 ------------- 168.057E+06 ------------- 336.127E+06 ------------- 0.1006 ------------- 998.583E-03
10. ------------- 170.E+06 ------------- 340.005E+06 ------------- 0.1006 ------------- 1.00211
as you can see stress peaks at 6.8 second and decrease after that. May I know how abaqus explicit reached that value? I heard explicit does not do iteration and it calculates later time from current step. Unknown values are obtained from information already known.