The TIA-222.G.3 standard says that the max tension on a single bolt (in a
baseplate attached to a pole) is calculated from the following formula:
1.02*pi*Mu/(n*Dbc) (assuming that there are at least 12 bolts and a minimal axial load is present)
Where:
Mu is the applied moment in inch-kips,
n is the number of bolts, and
Dbc is the bolt circle in inches
A dimensional analysis shows that the resulting answer is in kips of tension (or compression), but I cannot figure out how they derived the formula. TIA say that the bolt circle is treated like a ring of steel with a diameter equal to Dbc.
You can convert the total area of all the bolts into an equivalent area in a ring, and then calculate the section modulus of that hollow circle. Then you can do a M/S to get the max stress, which could then be applied to a single bolt to get its tension. However, I can't see where a formula that simply contains a pi/D ratio is anywere related to a section modulus.
Can anyone shed some light on this for me??
baseplate attached to a pole) is calculated from the following formula:
1.02*pi*Mu/(n*Dbc) (assuming that there are at least 12 bolts and a minimal axial load is present)
Where:
Mu is the applied moment in inch-kips,
n is the number of bolts, and
Dbc is the bolt circle in inches
A dimensional analysis shows that the resulting answer is in kips of tension (or compression), but I cannot figure out how they derived the formula. TIA say that the bolt circle is treated like a ring of steel with a diameter equal to Dbc.
You can convert the total area of all the bolts into an equivalent area in a ring, and then calculate the section modulus of that hollow circle. Then you can do a M/S to get the max stress, which could then be applied to a single bolt to get its tension. However, I can't see where a formula that simply contains a pi/D ratio is anywere related to a section modulus.
Can anyone shed some light on this for me??

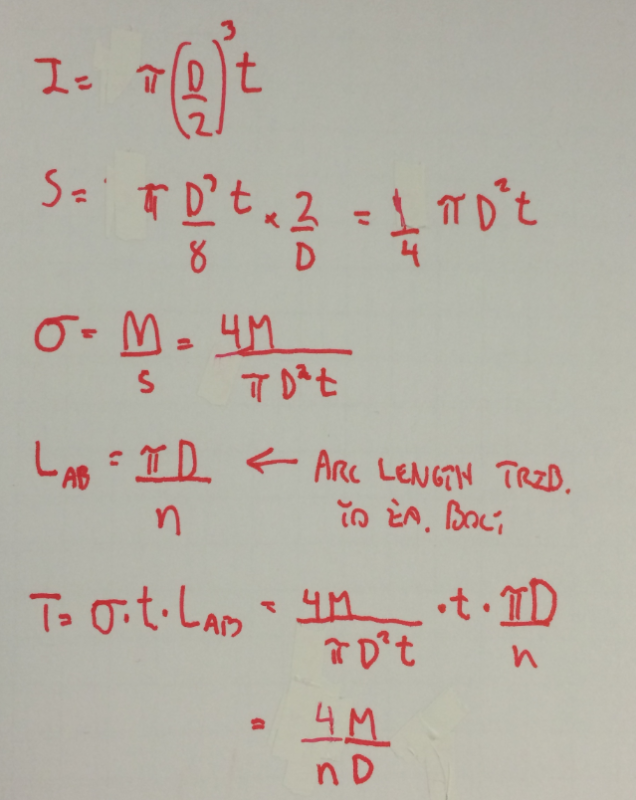
![[thanks2] [thanks2] [thanks2]](/data/assets/smilies/thanks2.gif)
