Hi everybody,
Can anyone comment my work, since I'm new in this are? I'm trying to perform SIMO analysis in MAtlab.
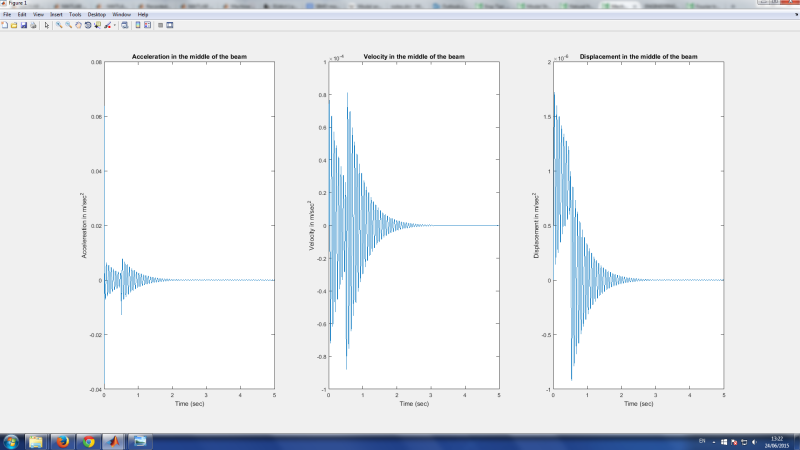
I have done an analysis of Euler-Bernouli beam subjected to square force in the middle of the beam in Matlab. Using Wilson's Theta numerical integration method I have calculated the beam response, e.g. accelerations, velocities and displacements for the applied excitation. Time step for calculation is 0.002sec. Load magnitude is 25kN and durations is 0.5 sec. The time sampling interval is 5 sec. The force is applied in the middle of the beam, what coincides with the 6th node.
Now I want to obtain point FRF. I know that FRF is the ratio of the beam response to applied loading, i.e. displacements to square force in frequency domain, but here are some unclarities how to obtain this in Matlab.
I'm not sure what should be the sampling frequency. Is it 1 over time step 0.002 for which I've calculated the beam response, or is it 1 over the time sampling interval of 5sec? I've used the time sampling interval, but I don't know is it correct.
Then, I have performed the fft of the displacements for the node where the load is acting and only for translational DOF. Fft of the force I've also done. The absolute values of both are calculated.
Here is the code which I have used for obtain the FRF's:
%% Calculation of beam response in the middle and applied force in frequency domain
Fs = 1/T; %Sampling frequency in Hertz
timeinterval = time; %time = (0:dt:T)
% FFT of displacement at 6th node for translational DOF and force vector
DISP = fft(displace(11, );
);
P = fft(Pn);
% Calculating absolute values of displacements and force in frequency
% domain
DISPabs = abs(DISP);
Pabs = abs(P);
displength = length(DISPabs)/2;
Displacement = DISPabs(1:displength);
Force = Pabs(1:displength);
% Calculating FRFs and plotting
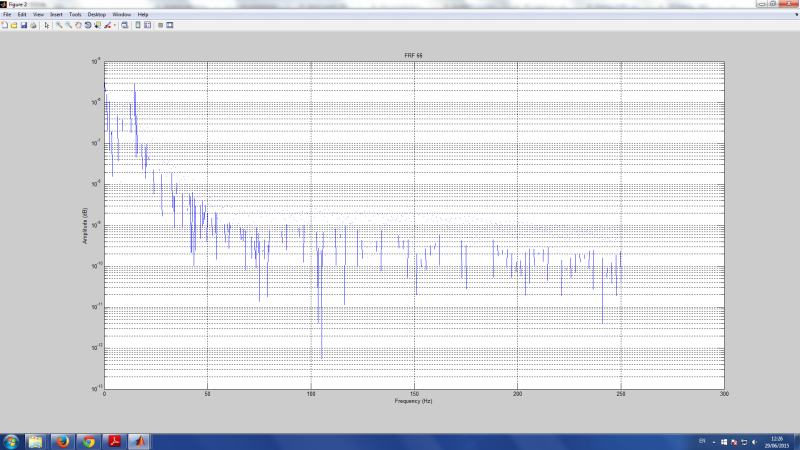
FRF66 = Displacement./Force;
Nyquist = Fs/2;
frequency = linspace(0,Nyquist,displength);
figure
semilogy(frequency,FRF66);
grid on
title ('FRF 66')
xlabel('Frequency (Hz)')
ylabel('Amplitude (dB)')
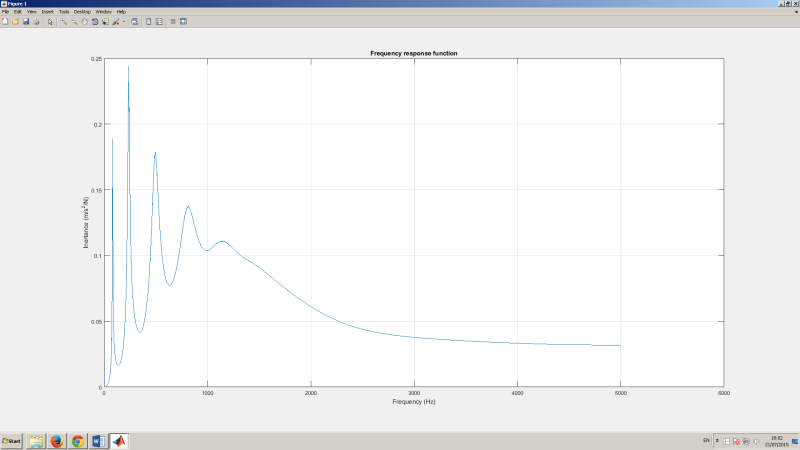
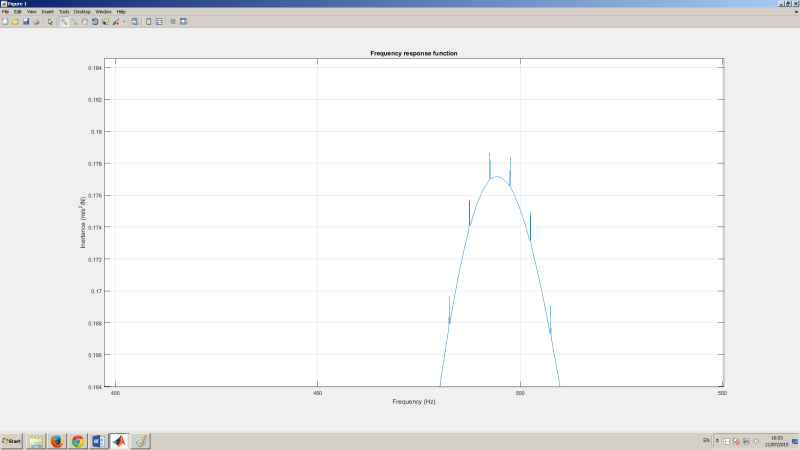
I have also attached the picture with the results of the beam response,
and picture of the FRF at node 6
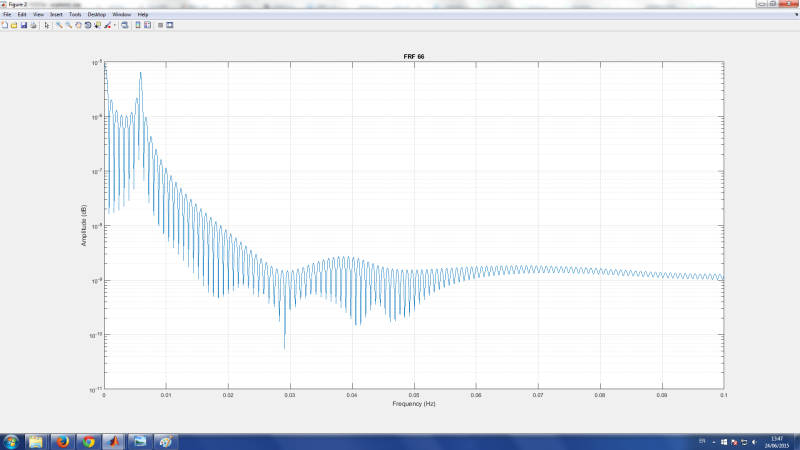
Would it be reasonable to calculate the power spectral density with periodogram or welch method instead of doing just fft?
Can anybody comment my work, because I don't know is this exact, am I going in the right way?
Please help!
Can anyone comment my work, since I'm new in this are? I'm trying to perform SIMO analysis in MAtlab.
I have done an analysis of Euler-Bernouli beam subjected to square force in the middle of the beam in Matlab. Using Wilson's Theta numerical integration method I have calculated the beam response, e.g. accelerations, velocities and displacements for the applied excitation. Time step for calculation is 0.002sec. Load magnitude is 25kN and durations is 0.5 sec. The time sampling interval is 5 sec. The force is applied in the middle of the beam, what coincides with the 6th node.
Now I want to obtain point FRF. I know that FRF is the ratio of the beam response to applied loading, i.e. displacements to square force in frequency domain, but here are some unclarities how to obtain this in Matlab.
I'm not sure what should be the sampling frequency. Is it 1 over time step 0.002 for which I've calculated the beam response, or is it 1 over the time sampling interval of 5sec? I've used the time sampling interval, but I don't know is it correct.
Then, I have performed the fft of the displacements for the node where the load is acting and only for translational DOF. Fft of the force I've also done. The absolute values of both are calculated.
Here is the code which I have used for obtain the FRF's:
%% Calculation of beam response in the middle and applied force in frequency domain
Fs = 1/T; %Sampling frequency in Hertz
timeinterval = time; %time = (0:dt:T)
% FFT of displacement at 6th node for translational DOF and force vector
DISP = fft(displace(11,
P = fft(Pn);
% Calculating absolute values of displacements and force in frequency
% domain
DISPabs = abs(DISP);
Pabs = abs(P);
displength = length(DISPabs)/2;
Displacement = DISPabs(1:displength);
Force = Pabs(1:displength);
% Calculating FRFs and plotting
FRF66 = Displacement./Force;
Nyquist = Fs/2;
frequency = linspace(0,Nyquist,displength);
figure
semilogy(frequency,FRF66);
grid on
title ('FRF 66')
xlabel('Frequency (Hz)')
ylabel('Amplitude (dB)')
I have also attached the picture with the results of the beam response,

and picture of the FRF at node 6

Would it be reasonable to calculate the power spectral density with periodogram or welch method instead of doing just fft?
Can anybody comment my work, because I don't know is this exact, am I going in the right way?
Please help!