Hello all,
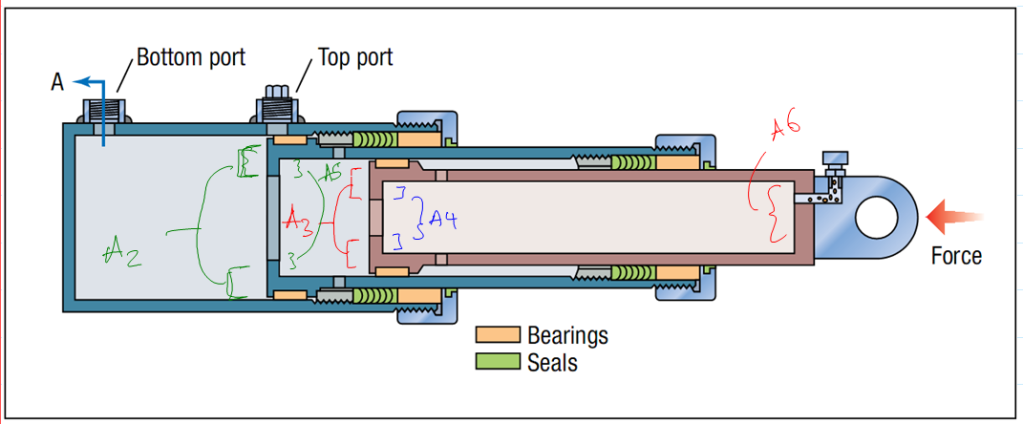
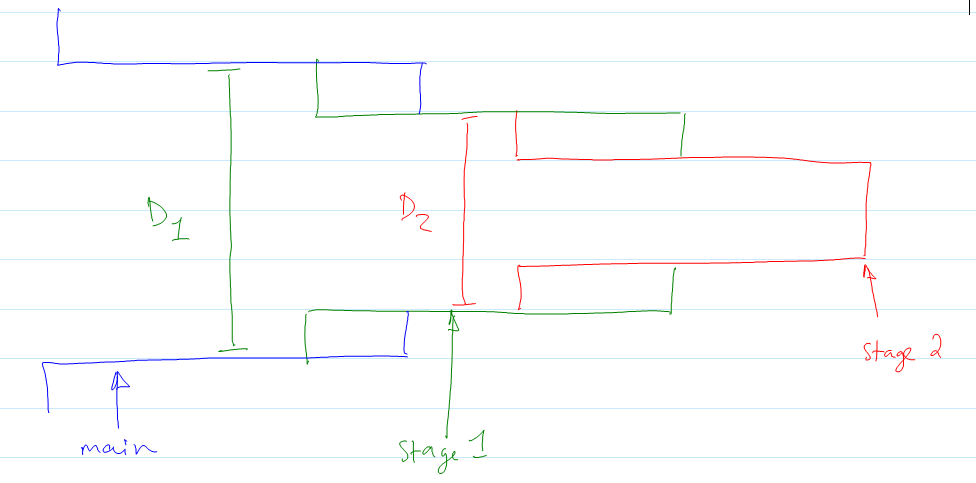
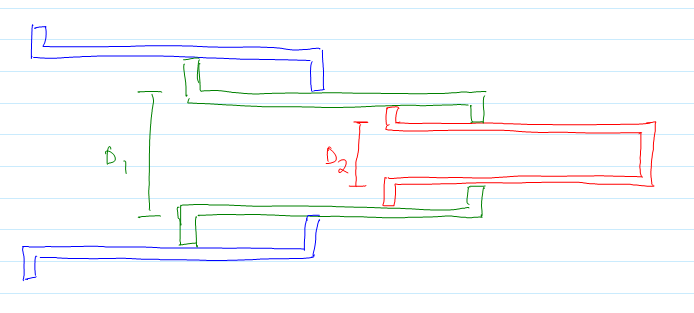
I am familiar with the method of calculating the required pressure in a hydraulic cylinder in order to generate a desired force: P = F/A, where A is the area of the piston. However, looking at cutaway drawings of telescopic cylinders shows that it is more complicated internally, with multiple pistons and each one letting fluid into the next. How would I go about relating the force and pressure in that situation?
Thanks
--Amr
I am familiar with the method of calculating the required pressure in a hydraulic cylinder in order to generate a desired force: P = F/A, where A is the area of the piston. However, looking at cutaway drawings of telescopic cylinders shows that it is more complicated internally, with multiple pistons and each one letting fluid into the next. How would I go about relating the force and pressure in that situation?
Thanks
--Amr