Spiral cmd 2

From what you described, a spiral sounds like the solution to your variable radius problem. But I believe the variation in the radius is linear, not logrithmic.

Could you provide a picture of what you want? Or at least provide some input parameters?

Another way to make the variable radius curve is with PARALLEL CURVE and LAW.

Make a LAW that defines the logrithmic variation in the radius (from R1 to R2). Then make a circle with a base radius of R1. Use PARALLEL CURVE to 'offset' from the base curve.

Probably, the easiest way to create a log spiral is to write some code using the parametric equation for a logarithmic spiral, and if I was doing that I'd write it in a VBA macro in Excel and then create the spiral from an external file, the only limitation being 500 points - if I recall.

But, if the code writing method is ruled out it can be done by making the (planar) spiral from a space curve. The V5 Spiral offers a increasing radius that only increases linearly (Archimedean), and the Helix Law is limited to either linear or 'S' type - but nothing more sophisticated. However, the Sweep tool allows the use of Advanced Laws.

I think an elegant solution is to create a single element, irrespective of the number of turns.

There are three parameters in a spiral, apart from defining the nature of growth:-

[ul]
[li]Start Radius[/li]
[li]End Radius[/li]
[li]Number of Revolutions[/li]
[/ul]
Click the small images to enlarge them...


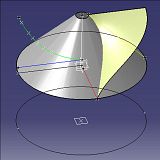
So I swept a helical surface along a line, using a pitch which increases according to a logarithmic law. This surface, which looks like an accelerating screw conveyor, intersects a cone, resulting in a conical helix with a log variable pitch.

If the semi-cone angle is 45 degrees then it is easier to visualise what is happening: the conical helix is going to re-mapped onto a plane - giving the required Spiral. This effective transformation is the key operation to getting the (multi-turn) log spiral - in one go.

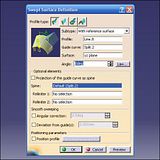
First thing to do is draw a Logarithm curve, because if we want a log law we've got to construct a log curve. I used the log values of 1 to 10, with unit increments (using a calculator), and shifted the decimal place over to scale them up by 100 - when creating a set of curves to put a spline through (#1). This gave a curve from (0,10) to (100,100), conveniently giving a delta Z of 90. This will represent 90 degrees in the sweep Angle input. A line then needs to connect the points (0,10) and (100,10) - this is the Law Reference and the log curve is the Law Definition (#4). With a default scale of 1, OK the Law.

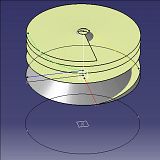
A line normal to an axis will generate the helical surface when it is wound along the axis by angle controlled by the log law (#5&#6). Another line, in the same plane, will be revolved to make a cone. This second line will go from a point that is the Start Radius to the End Radius - over the length of the axis.

At this stage I'd recommend setting this up with the law as it is: scale=1. It will have made a spiral over 90 degrees (#2), so edit the law by changing the scale to 4 - and the spiral will now do one complete turn (#3). Changing the scale by multiples of 4 will increase the number of turns, in this example there are 4 turns - so the scale will be 16 (#7). The Start and End Radii could also be edited by their respective point values - if needed.

Intersect the helix and the cone: this will give the conical helix (#8). Hide the two surfaces. Then project the conical helix on to a plane normal to the axis. This is the required Logarithmic Spiral (#9).

If the spiral needs to have a diminishing radius rather than an increasing one, then the helical surface can be flipped about its axial mid-point using a symmetry transform.

At first, this might appear to be a long-winded procedure, but the result will be an accurate solution, created from a few initial construction elements.

It's an interesting exercise in spatial thinking, what I usually call simply complex..!

If some other type of law is required, then an appropriate curve is drawn; this could be a parabola, cubic or a polynomial.

But certain curves, some are listed below, can be constructed using Kinematics - by putting a trace on a moving point, using a fine increment to generate plenty of points, and then running a spline through them.
[ul]
[li]Cycloid[/li]
[li]Involute - similar to log spiral[/li]
[li]Epitrochoid[/li]
[li]Hypotrochoid[/li]
[/ul]

First & Formost thankyou all for your responses and especially to Kapitan. Such a wonderful community! You truely are amazing in your through and thoughtful posts of information. I think I have a better sense of direction now to achieve my goal. I will post the final results upon completion in hopes that others may benefit as well. Again, Thankyou so very much for your time and energy.
J