pylfrm 30 Apr 19 01:15 said:
The direction of [x] is defined by the constraint of [v,w]. The direction of [y] is defined by the constraint of [u,w]. The direction of [z] is defined by the constraint of [u,v].
I think this is the key here. Ie: [x] cannot be fully constrained "everywhere" until [v,w] is constrained, same with [y] and [z]. Likewise a datum feature that constrains [v] or [w] is also involved in fully constraining [x] (again, rinse/repeat for [y] and [z]).
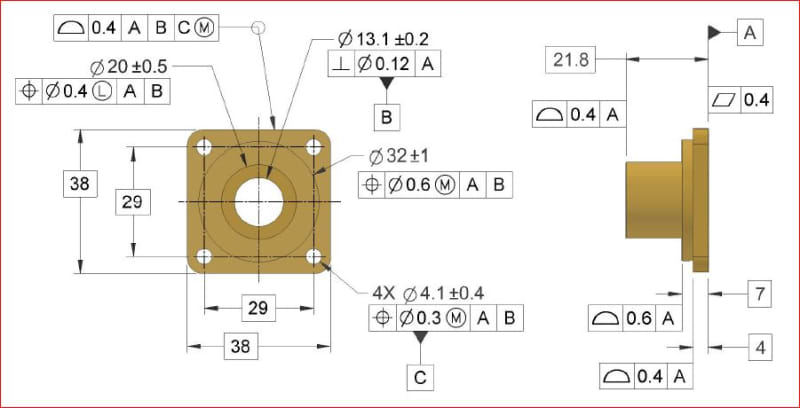
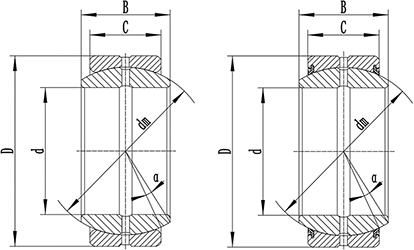
It seems to me that we can say something similar, with some restrictions, about the converse. Unless [v] or [w] has been constrained by a higher order datum feature, a datum feature that constrains [x] is also involved in fully constraining [v] or [w] (respectively). Again with the applicable rotational DOF with [y] and [z]. It took me a bit to figure out why I couldn't make a blanket statement about this as a result of the translation modifier - as this applies in the case of 4-19 with the translation modifier (higher order datum feature B which constrains [x,y] is involved in the constraint of [w] when C is applied) but not in your example of the spherical bearing (higher order datum feature A which constrains [x,y,z] is not involved in the constraint of [u,v]).
What I came up with is if you have a datum feature with a translation modifier which can constrain remaining rotational DOF of interest by itself (which is a width FOS* in the case of your bearing) then higher order datum features are not involved (in 4-19 B or C alone cannot constrain [w] so they must both be involved). That being said, and I'm going to preface this by saying that I am not 100% sure about this or that its a control that even makes sense, if we were to take 4-18 and apply a translation modifier to C (allowing translation in [y] ie: up/down) would the same still hold? My instinct says yes, but I have some doubt in my mind that is saying your spherical bearing example is a special case because of the arrangement of the datum features (datum feature simulators would surround the point/axis of rotation vs. offset as in 4-18).
As a final thought, now that I have dug into it - I am questioning some of the earlier logic. I can fully see how in 4-9 and 4-19 primary datum feature A is involved in constraint of [x,y], however I am now not so sure about [w]. I am trying to fit this into my thought process/logic outlined in the first part of this post (relationship between relative translation/rotation DOF constraint) - perhaps I am missing something and you can help me amend my understanding?
*Edit - I mistakenly stated planar feature, instead of a width FOS. If one side of the spherical bearing was (instead of the width) specified as the datum feature B, primary datum feature A would still be involved with constraint of [u,v]. I'm not so sure about other examples with planar features, or whether this statement would apply.
Apologies for the multiple edits.