Hello,
Could someone here help me understand the process of using NDS TR14 and how to apply it to the attached beam.
I don't think I understand the process. Do I look at this as 3 separate spans and find the maximum moment inside of each span as well as the quarter moments in each span for use in calculating Cb? If so, is the purpose of this to determine the controlling span for unbraced length? And then I use that Cb for all spans since it is the same beam?
Could someone here give me a understanding of how to approach this.
Another thing that confuses me is, this beam has inflection points so different portions of the beam will have top flange in compressions and sections will have the bottom flange in compression.
I guess I'm confused on how to break it all down for analysis.-- The loads probably don't require this level of detail but I would still like to know the approach for the future.
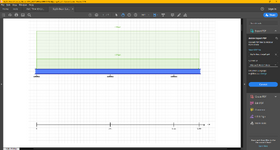
In my instance, this is a double 2x12 beam that has 2x10 joist framing into the side of it with joist hangers. The reaction points shown are actually 6x6 post. Decking is attached to the top edge of the beam.
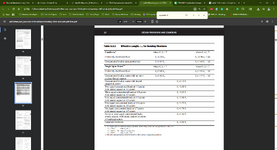
The attached report shows the points of +,- moment etc.
Could someone here help me understand the process of using NDS TR14 and how to apply it to the attached beam.
I don't think I understand the process. Do I look at this as 3 separate spans and find the maximum moment inside of each span as well as the quarter moments in each span for use in calculating Cb? If so, is the purpose of this to determine the controlling span for unbraced length? And then I use that Cb for all spans since it is the same beam?
Could someone here give me a understanding of how to approach this.
Another thing that confuses me is, this beam has inflection points so different portions of the beam will have top flange in compressions and sections will have the bottom flange in compression.
I guess I'm confused on how to break it all down for analysis.-- The loads probably don't require this level of detail but I would still like to know the approach for the future.
In my instance, this is a double 2x12 beam that has 2x10 joist framing into the side of it with joist hangers. The reaction points shown are actually 6x6 post. Decking is attached to the top edge of the beam.
The attached report shows the points of +,- moment etc.

Attachments
Last edited: