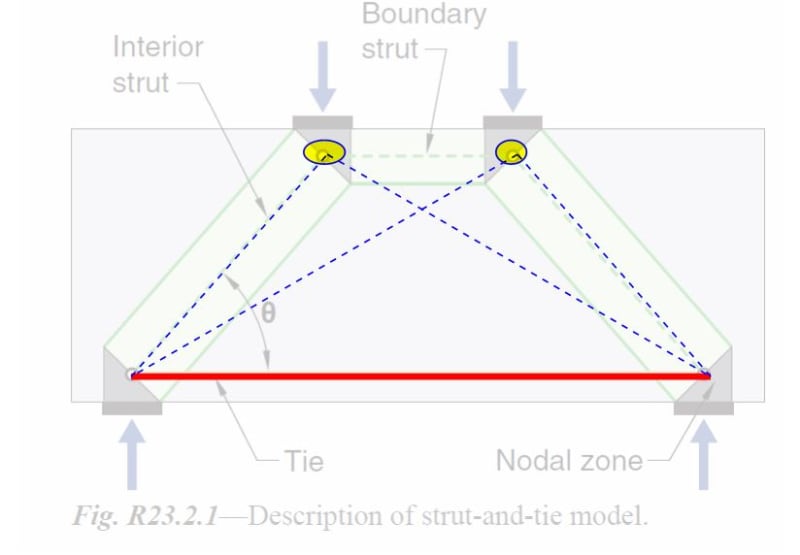
gusmurr said:
Stability is satisfied simply because everything is "braced" by the large mass of concrete.
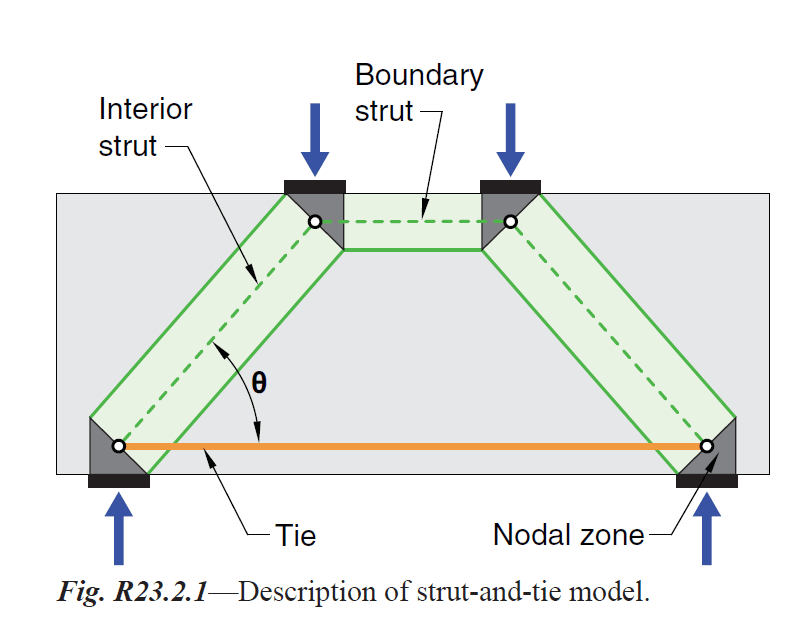
While it may feel more intellectually satisfying to add in the diagonal, I feel that gusmurr's comment above is the fundamental truth of the matter. The strut and tie method is a truss analogy and, like most analogies, it's imperfect. And perfect triangulation / explicit stability is one several ways in which it is imperfect. I believe that the stability of a model like this, put into equilibrium, is justified as follows:
1) Bracing loads for systems in equilibrium tend to be very small relative to the applied load.
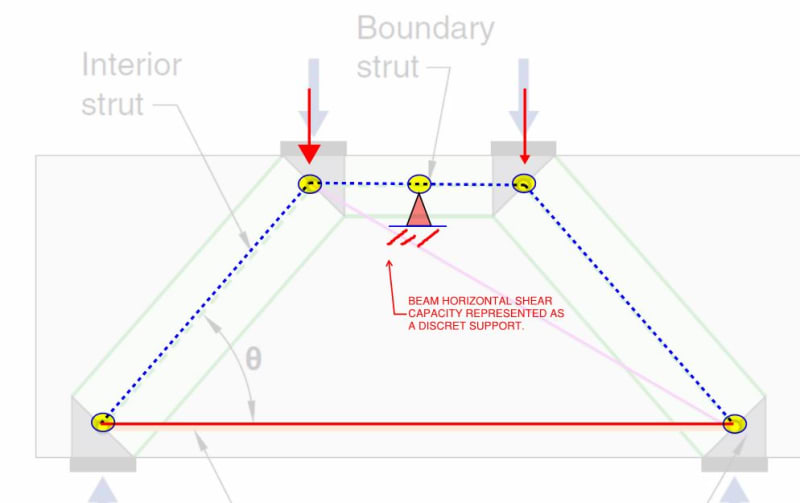
2) It's really the horizontal shear capacity of the beam stabilizing our fictional truss. and that capacity can be expected to be massive.
Were one to remove all of the concrete other than that included in the STM model, there would indeed be a problem and, most likley, a need for something like the diagonal.
Agent666 said:
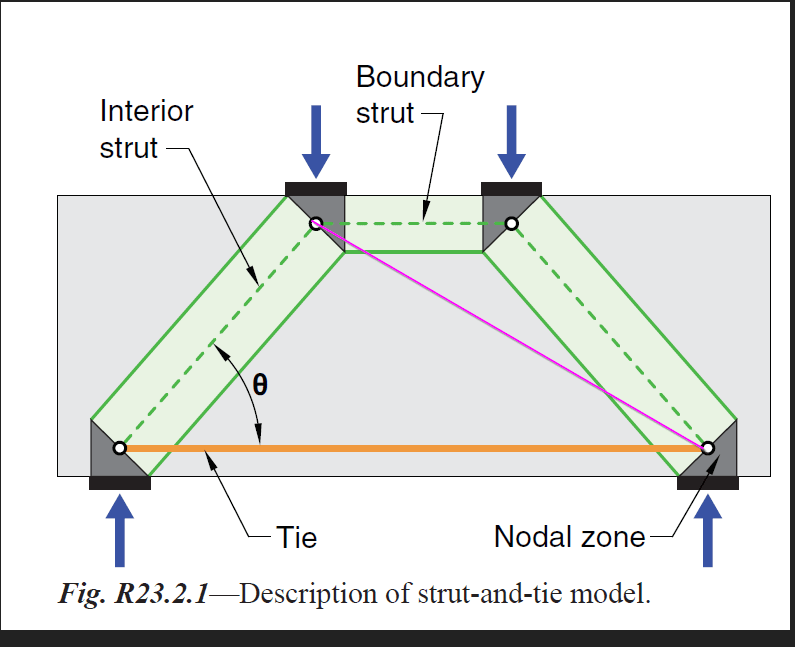
If the applied loads aren't equal then you'll need the additional diagonal won't you?
Certainly,
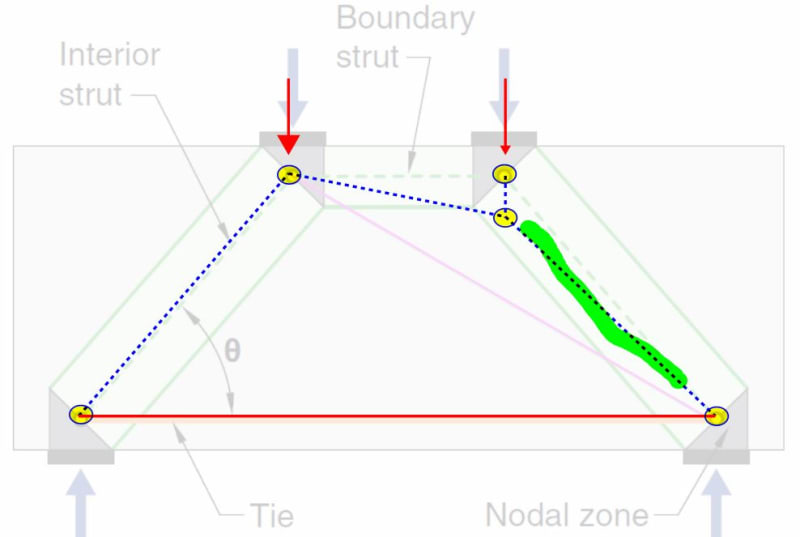
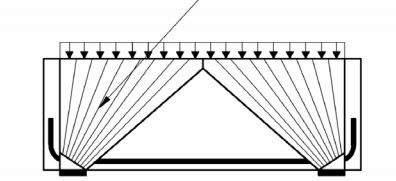
something must be done to put the model into static equilibrium. And adding the diagonal is one way to do that. Another way, I believe, is shown below. I see a couple of advantages with that approach.
1) A simpler model that might be a bit easier to prosecute at the nodes.
2) You'd not bump up against, potentially, a diagonal strut that would trigger too shallow of a strut angle (25 deg etc) in a way that may be spurious.
3) Taken in aggregate, the diagonal and the model below both capture the same, fundamental aspect of the stress field: the strut highlighted in green gets shallower.