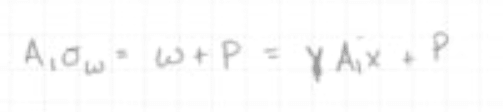Strength of Materials Part 1, Timoshenko, P8, Form of Equal Strength

[jpcrowd]

Hey All,

I'm revisiting classical stress analysis and working through Strength of Materials, Part 1 (3rd ed.) by Timoshenko. I'm currently stuck on problem 8, particularly with deriving equation (a). While the equation intuitively makes sense—where the change in area times the working stress is proportional to the weight of the change in volume—I'm having trouble proving it mathematically.

I've attached scans of the problem and two of my attempts at the derivation. Any insights or guidance on how to approach the derivation of equation (a) would be greatly appreciated! As of right now, I'm my best guess is my Answer 1 is correct and dA*dx is so small it goes to zero.

** Also clarifying I'm not a student asking for homework/project solutions. I'm not in school, just trying to improve as a structural analyst **

Determine the form of the pillar in Fig. 17 such that the stress in each cross section is just equal to working stress. The form satisfying this condition is called the form of equal strength.

 

[rb1957]

(a) is "just" saying that (on the LHS) the change in force on the the element (dA is the difference in area over the slide dx wide) = dA*sigma ...
is equal to (on the RHS) the weight of the volume of the slice = density*A*dx. which is pretty much what it says, no?

"Wir hoffen, dass dieses Mal alles gut gehen wird!"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.

 

[Snickster]

In your first two equations you have set up as if areas A1 and A2 were constant. They are constant on the left side of the equation but not constant on the right side but "A" is a function of "x". Total area to calculate weight is not therefore A1(x) or A2(x) on the right side but the summation of A(dx). Here is the correct derivation the way I see it:

 

[goutam_freelance]

What @Snickster has said is correct.

You can not consider the shape cylindrical even locally.

In your derivation you have considered A[sub]1[/sub] constant above m[sub]1[/sub]n[sub]1[/sub].

Engineers, think what we have done to the environment !

https://www.linkedin.com/in/goutam-das-59743b30/