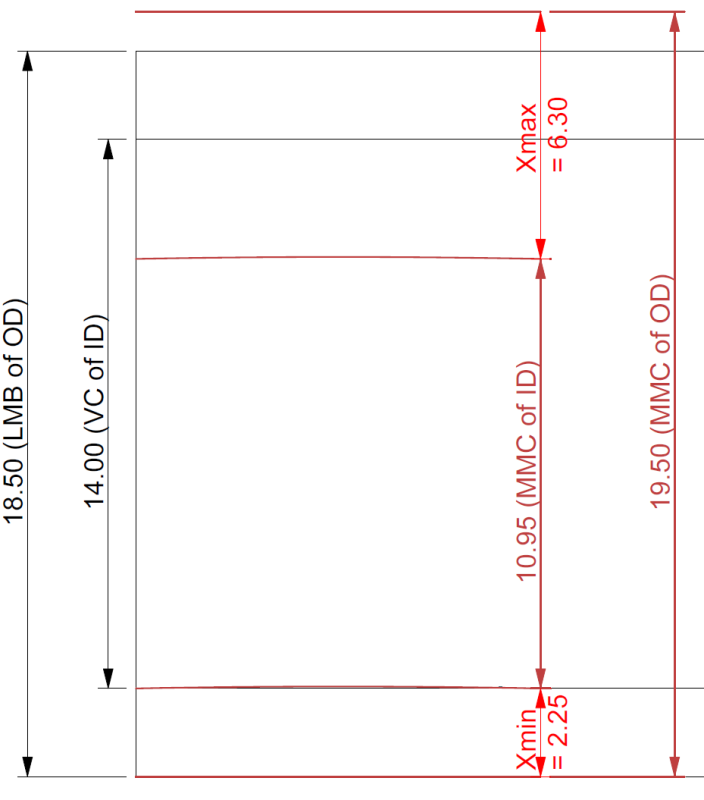
Just to be clear, I have not shown any of my derivations yet - I merely corrected 3DDave's derivation for Xmax and, to be honest, some pieces of it are still a mistery to me

For what it is worth, my preferred way of doing stacks is to use A.Krulikowski's method, but I noticed that the method isn't easy when it comes to explaining its logic/mechanics (especially to those who are not familiar with it). That is why in this forum I have always tried to explain my derivations by using additional sketch(es) and bringing the numbers down to simple equations. Here I will make no exception, although in this case the sketch looks pretty similar to Evan's graphic.
Side note #1:
I agree with everything that Evan said about lack of sufficient explanation on how to calculate LMB size for unrelated features of size in current Y14.5. From what I see the figure has been completely removed from the draft of new Y14.5, however there is one statement in the draft that changes the story a little bit, in my opinion. In para. 7.11.8 they say:
"When an LMB equal to LMC is the design requirement for a given datum feature, a zero geometric tolerance at LMC is specified to the datum feature [...]". They explain it using an example with secondary and tertiary datum features controlled with 0@LMC geometric tolerances, but that statement stays true for primary (unrelated) datum features too. In other words, if in OP sketch the datum feature A had had a zero straigthness at LMC applied (as a DML control), the LMB of A would have been 19.0. Without it the LMB is 18.5.
Side note #2:
Evan, my sincere apologies for not waiting with my reply until you corrected the typo in your post