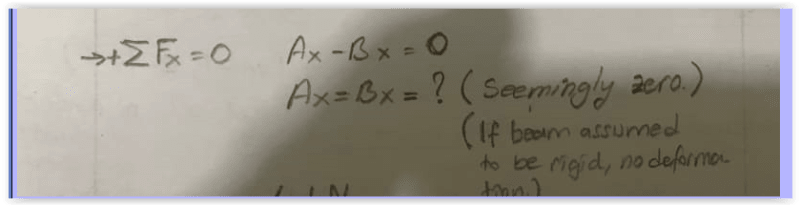Hi dear friends.I was reviewing and remembering very basic concepts of structural analysis course for my MSc entering exam since it had been 16 years after my graduate. While I was solving some problems on stability and determinacy of structures, I encountered a truss problem. While solving that one, I was trying to analyze the configuration of its members to try to figure out its internal stability visually. Then I failed, my answer, which was relied upon try to figure out the movement possibilities of joints using geometrical properties of them, was wrong. And then I started to try to understand what I did/thought wrong. So, at the end, the below problem has arised as a sample of my thinking way during this problem.
It is a simple supported beam at two ends with an internal hinge.
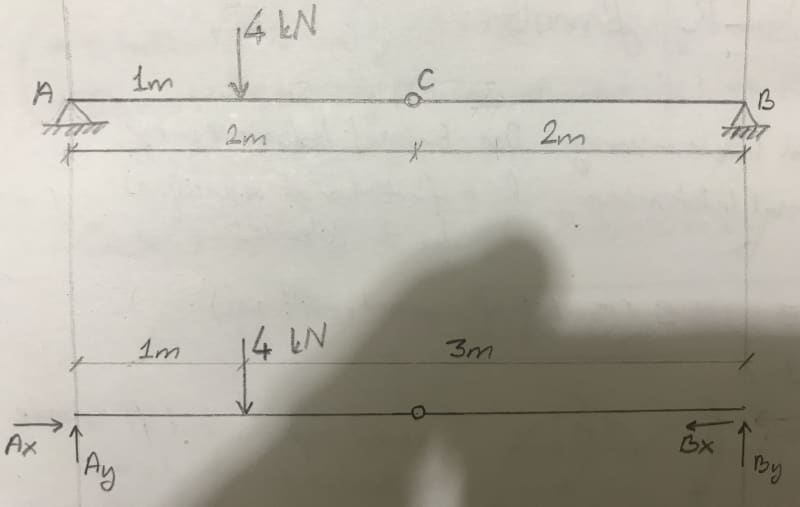
If you write equilibrium equations:
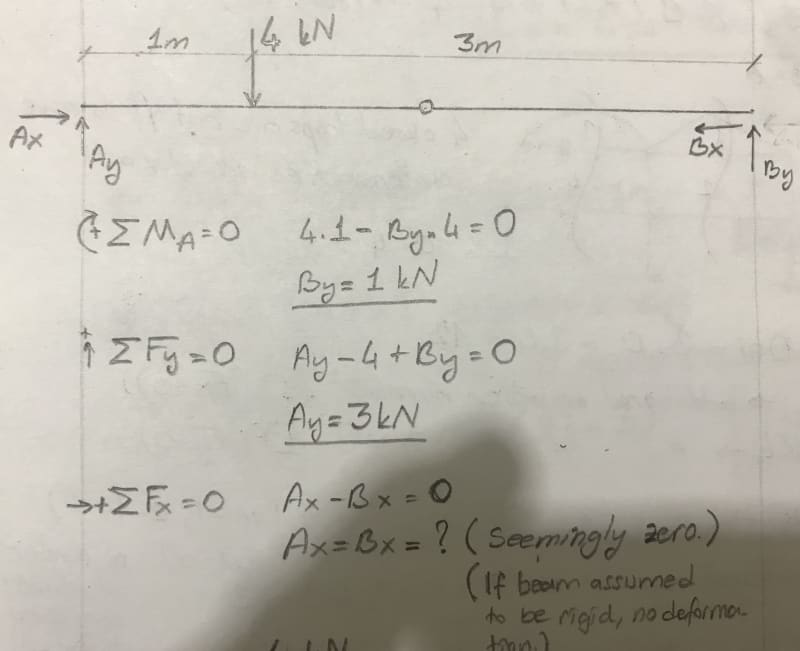
Then, for the section that is cut trough the hinge:

Since the equilibrium can never be satisfied in this way, I say it is not stable.
But, the below is another approach using geometry:
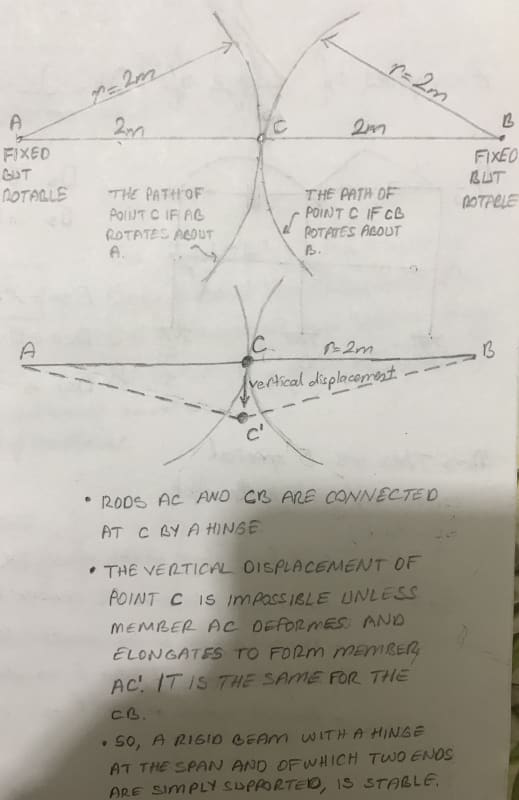
And this time, since it is impossible to move point C downwards without deforming the rods, and since the rods assumed to be rigid, then I conclude that this beam is stable.
My mind is mixed up a bit. But I think I may be overlooking some very basic assumptions about statics, structural analysis, etc.
Can you help me figuring out what I am overlooking or where I am wrong?
Thank you.
It is a simple supported beam at two ends with an internal hinge.

If you write equilibrium equations:
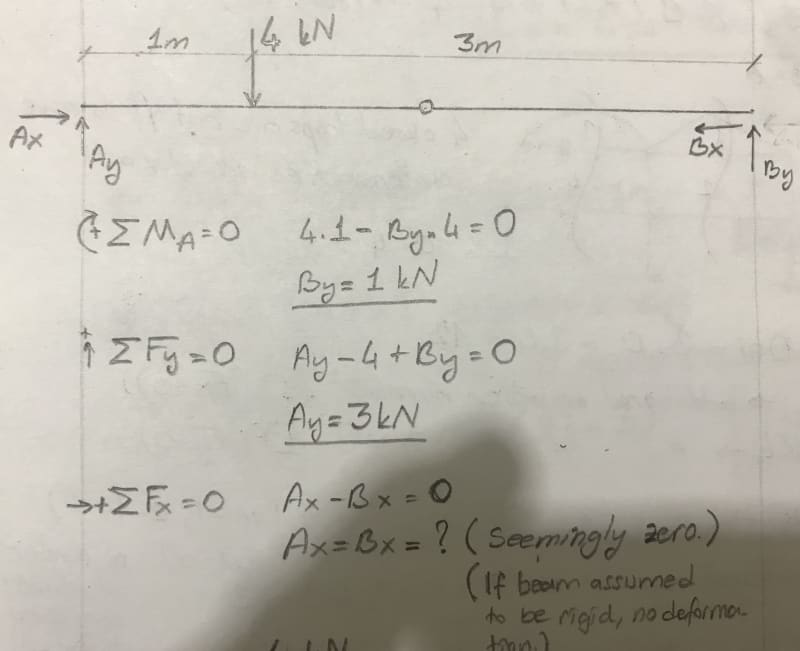
Then, for the section that is cut trough the hinge:

Since the equilibrium can never be satisfied in this way, I say it is not stable.
But, the below is another approach using geometry:

And this time, since it is impossible to move point C downwards without deforming the rods, and since the rods assumed to be rigid, then I conclude that this beam is stable.
My mind is mixed up a bit. But I think I may be overlooking some very basic assumptions about statics, structural analysis, etc.
Can you help me figuring out what I am overlooking or where I am wrong?
Thank you.