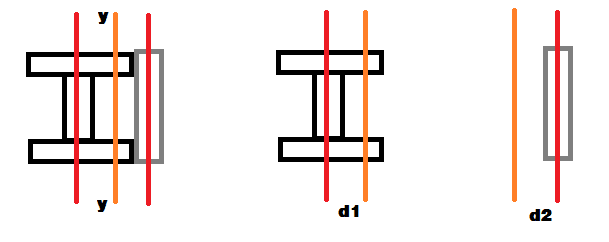Vonkrumm
Aerospace
- Feb 12, 2020
- 5
Hi Guys,
Just wondering how to work out the bending of a beam, that is reinforced with a flat-bar?
Or any piece of material for that matter (angle, C-section, ect.)
Example:
If you had a standard I-beam 30mm high, that had a piece of flatbar stuck to it's side - 30mm high (fixed to top and bottom of I-beam), how do you work out the moment of the area cross section?
Can you assume that the new area is simply the addition of the beam and flatbar areas?
(This is assuming that the flat-bar is fixed quite well to the I-beam.)
I know there are composite beams (and their associated calculation methods), but in my example above both materials are exactly the same....
Any help is much appreciated, and nice to join the forums!!!
Just wondering how to work out the bending of a beam, that is reinforced with a flat-bar?
Or any piece of material for that matter (angle, C-section, ect.)
Example:
If you had a standard I-beam 30mm high, that had a piece of flatbar stuck to it's side - 30mm high (fixed to top and bottom of I-beam), how do you work out the moment of the area cross section?
Can you assume that the new area is simply the addition of the beam and flatbar areas?
(This is assuming that the flat-bar is fixed quite well to the I-beam.)
I know there are composite beams (and their associated calculation methods), but in my example above both materials are exactly the same....
Any help is much appreciated, and nice to join the forums!!!