Navigation
Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
More options
Style variation
-
Congratulations MintJulep on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Shear ties compared to spiral reinforcement
- Thread starter livewire9
- Start date
- Status
- Not open for further replies.
Not if it is a round column. For shear strength, anchorage is crucial, and I can't see improving on continuous anchorage provided by spirals. If it is a spirally reinforced square column (as I first saw in a recent thread here), I don't know the answer.
For a standard square /rectangular stirrup with two legs you have 2 x bars worth of strength per unit spacing.
For a spiral at the same unit spacing the bars are equivalent to pi/2 bars worth of strength per unit spacing.
pi/4 is the 'efficiency' of a single bar in a circular spiral and you have two complete bars per spiral turn.
You generally need to reduce the spacing for the same overall size (say 600mm square vs 600mm diameter) but it depends on the member size obviously. Circular stirrups simply aren't as effective. But depends on the effective depth.
Just review your code equations and you will see this.
For a spiral at the same unit spacing the bars are equivalent to pi/2 bars worth of strength per unit spacing.
pi/4 is the 'efficiency' of a single bar in a circular spiral and you have two complete bars per spiral turn.
You generally need to reduce the spacing for the same overall size (say 600mm square vs 600mm diameter) but it depends on the member size obviously. Circular stirrups simply aren't as effective. But depends on the effective depth.
Just review your code equations and you will see this.
Link
check page 336 of the above link.
In New Zealand we have this formulation in our code, our code is based on ACI318 so I made the incorrect assumption that it was in there as well. But I see on checking ACI that its behind the times a bit in this respect.
Tomfh & hokie66, the point is that for a typical 45 degree shear crack/plane, not all bars in a circular member intersect the crack at 90 degrees (think of the bar crossing the 45 degree shear plane anywhere but the center of the member), this leads to a reduction in the 'efficiency' of the spiral when compared with typical ties in a rectangular member. In a rectangular member the bars cross the shear plane at 90 degrees, in a circular member this angle varies depending on where you take your slice through the section. Most codes including ACI have provisions for ties which are placed at some other angle than being vertical in a beam, they are not as effective if you tilt a stirrup over, its similar in concept to this and is the "correct" formulation.
I don't know what else to say if I haven't turned you into a believer!
check page 336 of the above link.
In New Zealand we have this formulation in our code, our code is based on ACI318 so I made the incorrect assumption that it was in there as well. But I see on checking ACI that its behind the times a bit in this respect.
Tomfh & hokie66, the point is that for a typical 45 degree shear crack/plane, not all bars in a circular member intersect the crack at 90 degrees (think of the bar crossing the 45 degree shear plane anywhere but the center of the member), this leads to a reduction in the 'efficiency' of the spiral when compared with typical ties in a rectangular member. In a rectangular member the bars cross the shear plane at 90 degrees, in a circular member this angle varies depending on where you take your slice through the section. Most codes including ACI have provisions for ties which are placed at some other angle than being vertical in a beam, they are not as effective if you tilt a stirrup over, its similar in concept to this and is the "correct" formulation.
I don't know what else to say if I haven't turned you into a believer!
Not a believer. You are correct that the spiral results in the shear reinforcement crossing the crack at different angles, but half are better, half are worse. Nothing we do in structural engineering is precise, so spirals are good enough for me. Not that I don't respect the work of Priestly et.al...maybe it is just that I don't work in a seismically active area.
@Agent666: I suspect that hokie66 is discussing the effect that the pitch has on orienting the spiral ties relative to the assumed shear cracks whereas you are discussing the effect that the curvature of the spiral ties has on orienting them relative to the assumed shear crack. Different planes. I believe that both "inefficiencies" are valid.
@Hokie: before cracking, stirrups are most effective when oriented perpendicular to the shear cracks that they cross. However, once a crack has formed, the optimal orientation for a stirrup is vertical, or perpendicular to the longitudinal axis of the remember, correct? My point being that I believe that the pitch of the spirals is always a detriment to their ULS carrying capacity and never an asset.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
@Hokie: before cracking, stirrups are most effective when oriented perpendicular to the shear cracks that they cross. However, once a crack has formed, the optimal orientation for a stirrup is vertical, or perpendicular to the longitudinal axis of the remember, correct? My point being that I believe that the pitch of the spirals is always a detriment to their ULS carrying capacity and never an asset.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
I don't buy that either. Reinforcement perpendicular to a crack is better than at some angle to it. So I agree that half the bars are not as effective. But the benefit of essentially infinite development, as well as the better confining of the core concrete, overcome the angle problems, in my opinion.
Think in terms of the strength developed across any 45 degree crack as being governed by the 'shorter' portion of circular bar on the other side of the crack (the smaller semicircular part) and the angle it makes in plan with the crack line across the section. Realising this you can't have more capacity from the other half of the spiral simply because it has better anchorage. The force you can develop perpendicular to the direction of loading depends on the angle the bar crosses the shear plane. This is different for all bars crossing the shear plane.
So it's not a matter of taking the full strength of each bar, some are simply less efficient.
So it's not a matter of taking the full strength of each bar, some are simply less efficient.
hokie66 said:I don't buy that either. Reinforcement perpendicular to a crack is better than at some angle to it.
ACI would seem to agree with you based on their inclined stirrup capacity equation. @!@@&?@!!#$%!@#%!!!. Just when I was gearing up for a nice, relaxing weekend. Now, for the bazillionth time, I'm back to not understanding concrete shear.
Can you explain to me why inclined stirrups would be more efficient in a post-cracked state where the principle stresses have already dissipated due to cracking? See my sketch "A" below. Conceived of in typical modified truss fashion, I would certainly expect vertical ties to be the most efficient. Help!
Sketch "B" below illustrates my understanding of the phenomenon that Agent666, has been describing.
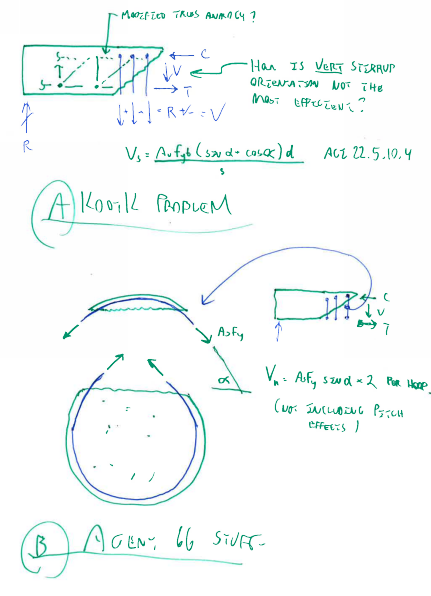
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
nonplussed
Structural
KootK said:Can you explain to me why inclined stirrups would be more efficient in a post-cracked state where the principle stresses have already dissipated due to cracking? See my sketch "A" below. Conceived of in typical modified truss fashion, I would certainly expect vertical ties to be the most efficient. Help!
Placing the stirrups at an inclined angle simply makes the concrete strut intersect more stirrups. This means 'Av' in your equation increases (or 's' decreases, whichever way you want to look at it). Assuming a concrete strut at 45 degrees, placing stirrups at 45 degrees perpendicular to the strut would be the most efficient and increase your 'Vs' by sqrt(2). It is easier to visualize if you do the opposite and consider inclining the stirrups the other way to be parallel to the strut; this would obviously reduce your strut efficiency to 0.
nonplussed
Structural
To clarify, when I say 'placing stirrups at 45 degrees perpendicular to the strut', I mean the stirrups and strut are perpendicular, with the strut being at 45deg from vertical and the stirrups being 45deg from the vertical the other direction.
Back again. I'll let nonplussed argue the truss analogy. There is no unique truss analogy.
At last, I get what Agent666 has been saying, but don't know how they came up with pi/2 bars (that might be more apparent if I had pages 335-337 of the reference). Regardless of the stirrup orientation, you can't have all the bars cross a given crack at the ideal position, which would be at the section centroid where the shear stress is greatest.
At last, I get what Agent666 has been saying, but don't know how they came up with pi/2 bars (that might be more apparent if I had pages 335-337 of the reference). Regardless of the stirrup orientation, you can't have all the bars cross a given crack at the ideal position, which would be at the section centroid where the shear stress is greatest.
- Thread starter
- #18
You're most welcome LiveWire9. I hope that you don't mind our following some tangents here as, in the process of attempting to answer your question, we have discovered some interesting questions of our own.
Yes, this is exactly it! Thanks for setting me straight.
@Hokie:
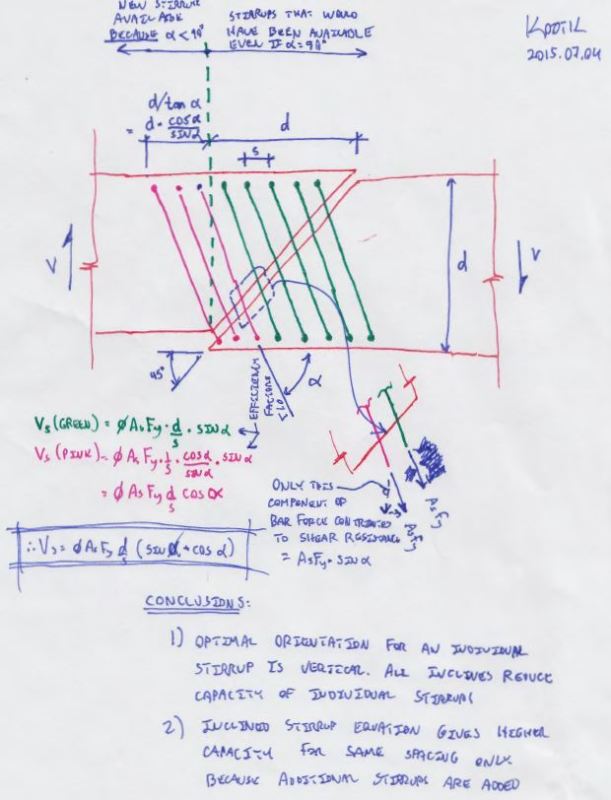
Using nonplussed's guidance, I've attempted my own derivation of the ACI inclined stirrups equation (below and attached). No doubt I could have just found it in a textbook if I had the right one. Anyhow, here are the conclusions that I've drawn from the derivation:
1) The sin term may be thought of as representing the stirrups that would have been available even if there were no incline. The capacity of those stirrups is multiplied by the sine of the incline angle to reduce their effectiveness.
2) The cos term may be thought of as representing the extra stirrups that cross the shear crack as a result of the incline. The capacity of these stirrups, too, are multiplied by the sine of the incline angle to reduce their effectiveness. This multiplication cancels out in the mathematics of determining the extra tie area available however.
3) The ACI equation for inclined stirrups shows an increase in capacity relative to perpendicular stirrups only because more stirrups become involved, not because individual stirrups are more effective when oriented more perpendicular to the anticipated angle of the shear crack.
4) The derivation of the ACI inclined stirrup equation suggests that the optimal orientation for stirrups is perpendicular to the longitudinal axis of the member. All other orientations, including perpendicular to the shear crack, are inferior and and that inefficiency is quantified by multiplying capacity by the sine of the angle that the stirrups make with the direction of the applied shear.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
nonplussed said:Placing the stirrups at an inclined angle simply makes the concrete strut intersect more stirrups.
Yes, this is exactly it! Thanks for setting me straight.
@Hokie:
Using nonplussed's guidance, I've attempted my own derivation of the ACI inclined stirrups equation (below and attached). No doubt I could have just found it in a textbook if I had the right one. Anyhow, here are the conclusions that I've drawn from the derivation:
1) The sin term may be thought of as representing the stirrups that would have been available even if there were no incline. The capacity of those stirrups is multiplied by the sine of the incline angle to reduce their effectiveness.
2) The cos term may be thought of as representing the extra stirrups that cross the shear crack as a result of the incline. The capacity of these stirrups, too, are multiplied by the sine of the incline angle to reduce their effectiveness. This multiplication cancels out in the mathematics of determining the extra tie area available however.
3) The ACI equation for inclined stirrups shows an increase in capacity relative to perpendicular stirrups only because more stirrups become involved, not because individual stirrups are more effective when oriented more perpendicular to the anticipated angle of the shear crack.
4) The derivation of the ACI inclined stirrup equation suggests that the optimal orientation for stirrups is perpendicular to the longitudinal axis of the member. All other orientations, including perpendicular to the shear crack, are inferior and and that inefficiency is quantified by multiplying capacity by the sine of the angle that the stirrups make with the direction of the applied shear.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
- Status
- Not open for further replies.
Similar threads
- Question
- Replies
- 16
- Views
- 12K
- Replies
- 1
- Views
- 2K
- Locked
- Question
- Replies
- 3
- Views
- 4K
- Locked
- Question
- Replies
- 1
- Views
- 2K
- Replies
- 124
- Views
- 34K
