Shear Center of Solid Section 2

[cal91]

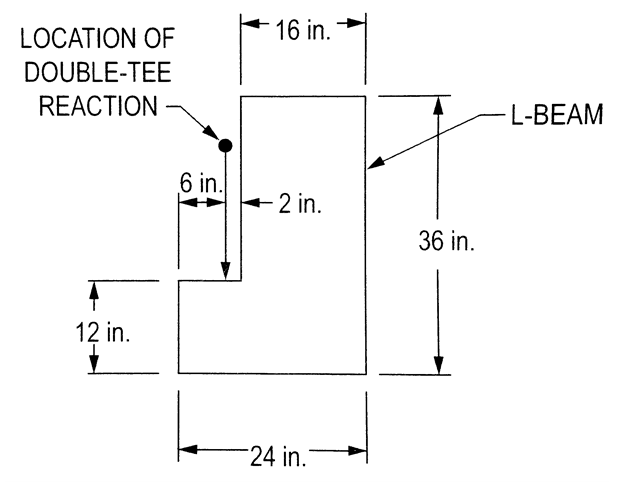
In the NCEES Practice Exam I was reviewing this problem, where the torsion due to the reaction is asked for. The solution calculated the eccentricity with respect to the center of gravity.

I would've thought that the eccentricity would be with respect to the shear center...

For solid sections, is the shear center the center of gravity? If not, how do you calculate it?

All of the resources I have (text books, internet) only provide information for thin wall sections, not solid sections for calculating shear centers. Does anyone know of a source for solid sections?

Thanks

 

[rb1957]

how could you do that in an exam ?

another day in paradise, or is paradise one day closer ?

 

[cal91]

Assume the shear center is at the centroid, I guess. Thats what the solution to the NCEES problem did!

Unless you're amazingly quick at finite element by hand.

 

[rb1957]

that's the problem with exam questions ... are they trying to trip you up over things you'd ignore ?

if you state "assume shear center = centroid", are they going to respond "-50% for simplistic assumption" ?

question to you guys who work in this field ... is this a "good" question ? is this something you see at work ?

another day in paradise, or is paradise one day closer ?

 

[cal91]

I personally don't think it's a good question. It doesn't test your understanding of torsion because you get the right answer with a wrong assumption.

It would be better if it stated the coordinates of the shear center as well as the coordinates of the centroid, and then had a wrong answer that you would arrive at had you taken the eccentricity with respect to the centroid.

The question asks for the ultimate torsion produced by the load. The answers are (k-ft)

A) 18.7
B) 20.7
C) 28.6
D) 34.5

using centroid, you get the "correct" answer of 28.6 k.

Using the actual shear center, you see that the "correct" answer is unconservative as the exact answer should be 35.1 k.

Not only that, but if you did the exact method somehow, you would choose D) and get that problem wrong.


This is a frustration I've dealt with in school - poorly written tests question. Many times you need to think, "okay what assumptions did the test writer make that they didn't state? What were they thinking when they wrote this"

I'm actually an excellent test taker, but some of that is because I've learned how to deal with situations like these, which doesn't have much (if any) real world application.

 

[cal91]

And if I were designing this beam, I would probably locate the actual shear center to get the eccentricity to make sure that I'm covered. I can't tell by inspection if the torque is substantial enough or not to include it.

I don't have near the experience that others on this forum have, and they might know it won't make a difference in the design and ignore the eccentricity all together.

 

[KootK]

I also feel that it's a poorly designed question. It will tend to bait deep thinkers in to trying too hard and, in all likelihood, loosing points as a result. In the defense of the exam writers, however, I could see it being surprisingly difficult to generate robust questions.

It can be quite frustrating trying properly calibrate your level of detail to match that of the examination questions.

I remember an exam question that was a moment loaded shear wall with boundary columns on each end. The columns sat on big concentric pad footings and there was an itty bitty strip footing under the wall connecting the columns. They wanted the max bearing pressure under the footings. I thought to myself "don't over think this, do what you'd do in practice". So figured out the compression chord reaction and divided it by the footing area to get a uniform bearing pressure on that end.

Years later, I saw the same question show up in a practice exam a that a colleague was working through. As it turns out, I got it wrong. The right answer was to treat the two pad footings and the strip footing as a composite section for the purpose of determining the max stress. Just like how you'd figure f_b for a wide flange in flexure. Go. Figure.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[haynewp]

See page 81 and 125, not thin walled members. Why is this incorrect?

http://www.pci.org/uploadedFiles/Si...nal/1984/DOI_Articles/jl-84-march-april-5.pdf

 

[cal91]

I guess I don't KNOW it's incorrect. I don't have access to the derivations. My hunch is that if you went through the derivations (anyone have the ROARK book?) that you would come accross the uniform shear stress across the thickness assumption. Which falls apart when b/t gets large.

Maybe in 1984 this was the best method for a quick approximation of the shear center? I don't know. I wasn't born yet

Unfortunately, this method does disagree with the section property calculator provided by avscorria, so one of the is wrong.

 

[cal91]

I just ran into a similar situation to KootK.

One of the practice problems in the same NCEES book asks for the moment capacity of a W10x22 Steel beam spanning 20 feet braced at ends and 10 foot mark. There is a point load at the 12 foot mark.

Answers are (k-ft)

A) 68
B) 76
C) 84
D) 97

Looking at plastic yielding, answer is 97. Looking at LTB, and conservatively taking Cb = 1, the answer is 76. Solving for Cb= 1.43 justifies using the full plastic moment capacity. Answer is 97.

If you went the extra mile you got the answer wrong. B) is the "correct" answer.

 

[mike20793]

I think the intent of that problem was to use Table 3-10 which assumes Cb=1.0. But it is misleading throwing in the location of the point load. If I remember my PE exam correctly, if it's not a one step calculation, you are probably doing more work than needed.

 

[cal91]

Mike -exactly. Why throw in the point load? If they aren't looking for a Cb>1, then the loading doesn't matter and shouldn't be included.

Otherwise you can still use Table 3-10 and multiply the value by Cb, then take the minimum between that and the plastic moment.

This is what frustrates me about many multiple choice test problems. It's not just about what you know, but also about you "calibrating your level of detail to match that of the examination questions" as KootK stated.

If you unfortunately GUESS the wrong level of detail, then you get the problem wrong. Obviously free response is better at eliminating this.

Side note, my teacher introduced Table 3-10 to us as the haystack. The member you are looking for is the needle.

 

[KootK]

I also had to calc the tension in a diaphragm chord to column connection with the columns located at 1/3 points along the diaphragm span. One set of calcs to check that the true Tf at the 1/3 points wasn't an option and another calc to do the WL^2/8 version which was the right answer. Again, time that I could have used elsewhere if I wasn't just so darn keen.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[cal91]

And yet another one on this same stinkin practice exam...

concrete slab spanning (6) 9'-0" bays. Maximum negative moment according to ACI 318 alternate to frame analysis?

Do you use wl^2/10 for negative moment at exterior face of first interior support, or wl^2/12 for ALL supports?

I got it wrong by being conservative and using wl^2/10. (only wl^2/12 required since slab span < 10')

It's a hard life for an engineer...

 

[haynewp]

It still seems to me like the shear will be divided relative to the stiffness of the parts, whether the shear distribution is uniform across the width of those parts or not. Similar to distributing forces in shear walls for a rigid diaphragm building. You can get real specific with FE and all that, but in practice this what I would use for a case like figuring out where to pick up an L shaped prestress members during erection. The "old" 1984 paper and Timoshenko book way and not an FE program.

 

[cal91]

I don't think a problem will arise from doing it that way, but to have the most accuracy I would resort to the section property calculator.

And my intent for throwing out the 1984 date was not to insult your source, but to offer an explanation why they used that method. I doubt section property calculators existed in 1984. Then again who knows.

 

[haynewp]

I thought it was funny because it made me feel old and not as making the reference less valid.