I've written a Pushover Analysis program for 2D Plane Frame structures. It captures the "red" part of the graph shown below (which includes all displacements up until the maximum force), and I'm trying to expand it to capture the "blue" part as well (which includes all displacements past the maximum force up until the tangent stiffness matrix is singular).
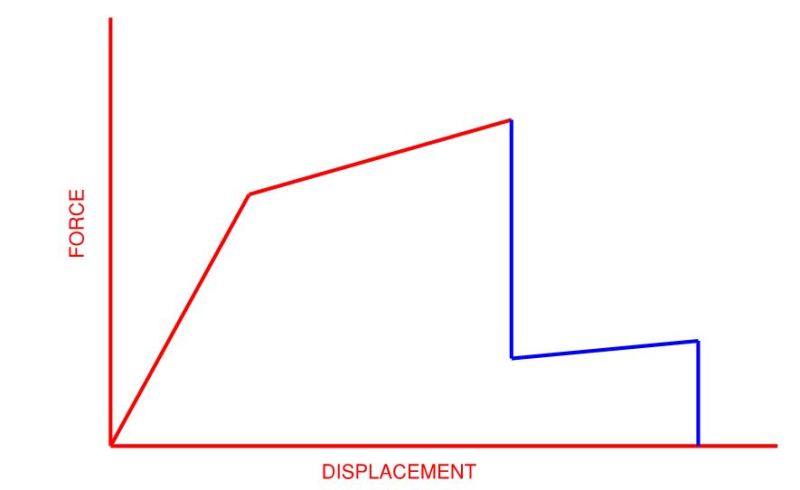
My program inputs a force and runs a nonlinear analysis, iterating until there is convergence. It then increments the force and repeats the analysis. Each force increment is stored as a data point on the Pushover graph. This works well for the displacements that are less than the "maximum force" displacement (where the red line turns to blue below).
How can I get the force required for further displacements? I can't wrap my head around it... The way the analysis works is I input a Force, and return a displacement... But it seems I need to input a displacement and get the resulting force?
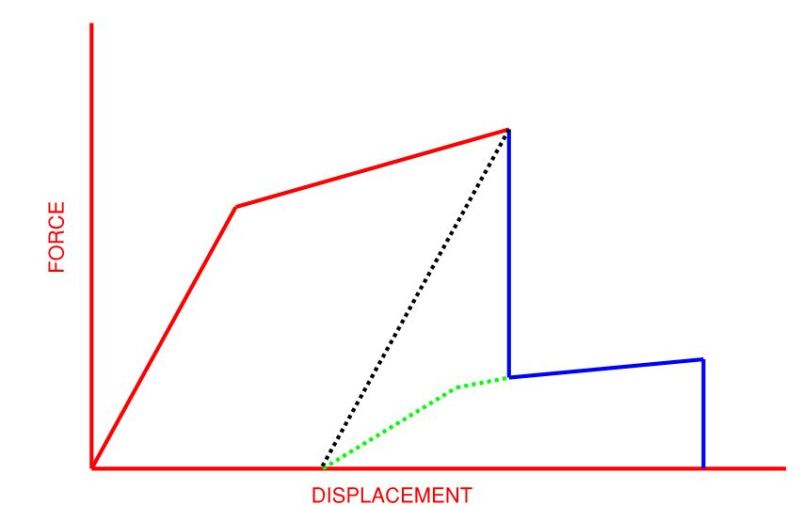
The only way I can think of is to increment the force until the displacement blows up, and save the displacements on the iteration right before the displacements blow up. I then set the force vector back to zero on the pre-blown up displacements and iterate until convergence (dashed black line below). From there I again increment the force and find the corresponding displacement (dashed green line below). I would have to do this process multiple times for each time a new "maximum force" happens before the tangent stiffness matrix is singular.
I've tried this way and haven't gotten it to work. It feels too messy anyways.
Maybe I don't understand the process correctly. Is there a simpler way, where I can somehow increment the displacement and find the force that would correspond to that diplacement? Does anyone have a good reference for nonlinear pushover analyses?

My program inputs a force and runs a nonlinear analysis, iterating until there is convergence. It then increments the force and repeats the analysis. Each force increment is stored as a data point on the Pushover graph. This works well for the displacements that are less than the "maximum force" displacement (where the red line turns to blue below).
How can I get the force required for further displacements? I can't wrap my head around it... The way the analysis works is I input a Force, and return a displacement... But it seems I need to input a displacement and get the resulting force?
The only way I can think of is to increment the force until the displacement blows up, and save the displacements on the iteration right before the displacements blow up. I then set the force vector back to zero on the pre-blown up displacements and iterate until convergence (dashed black line below). From there I again increment the force and find the corresponding displacement (dashed green line below). I would have to do this process multiple times for each time a new "maximum force" happens before the tangent stiffness matrix is singular.

I've tried this way and haven't gotten it to work. It feels too messy anyways.
Maybe I don't understand the process correctly. Is there a simpler way, where I can somehow increment the displacement and find the force that would correspond to that diplacement? Does anyone have a good reference for nonlinear pushover analyses?
