I suggest you find a good book on the stiffness matrix methods, here is a good free one:
Link - MASTAN2
First using Bones206 example:
For the 24" (tall) x 18" (wide) beam assuming F'c= 3000 psi and no stiffness reduction
Code:
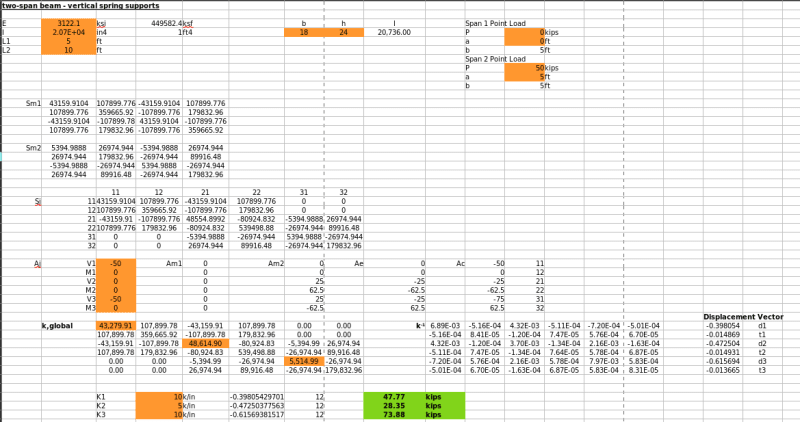
E 3122.1 ksi 449582.4 ksf
I 20736 in4 1 ft4
L1 5 ft
L2 10 ft
For all of the below matrices length has been taken as feet for consitency
The stiffness matrix for the 5 ft span beam is:
Code:
43159.9104 107899.776 -43159.9104 107899.776
107899.776 359665.92 -107899.776 179832.96
-43159.9104 -107899.776 43159.9104 -107899.776
107899.776 179832.96 -107899.776 359665.92
The stiffness matrix for the 10 ft span beam is:
Code:
5394.9888 26974.944 -5394.9888 26974.944
26974.944 179832.96 -26974.944 89916.48
-5394.9888 -26974.944 5394.9888 -26974.944
26974.944 89916.48 -26974.944 179832.96
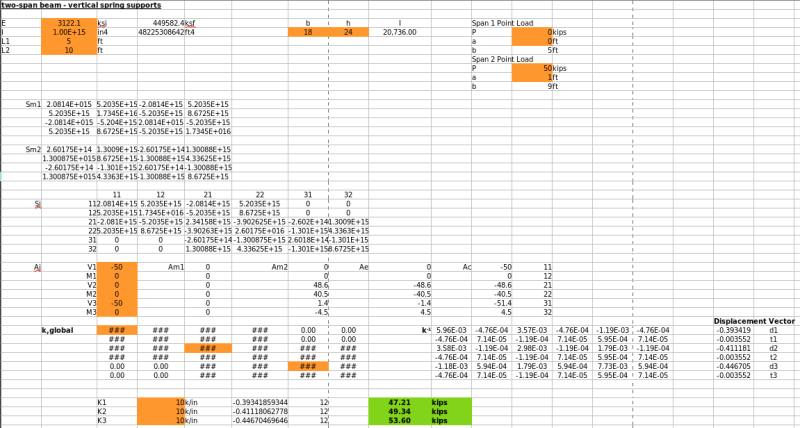
The global system stiffness matrix inclusive of the Pile Springs is, Kglobal:
Code:
43279.9104 107899.776 -43159.9104 107899.776 0 0
107899.776 359665.92 -107899.776 179832.96 0 0
-43159.9104 -107899.776 48674.8992 -80924.832 -5394.9888 26974.944
107899.776 179832.96 -80924.832 539498.88 -26974.944 89916.48
0 0 -5394.9888 -26974.944 5514.9888 -26974.944
0 0 26974.944 89916.48 -26974.944 179832.96
Because we are looking at this as a 2D problem and the vertical supports are springs then all joint displacements are unknown, and we know the joint loading is 50 kips at each joint. P*Kglobal^-1 = delta
Kglobal^-1:
Code:
0.005974863434211 -0.000490054673319 0.003537704848684 -0.000482185804678 -0.001179234949561 -0.000466448067397
-0.000490054673319 8.33763749299879E-05 -9.82513233548591E-05 7.38899760184168E-05 0.000588305996674 6.60386099950961E-05
0.003537704848684 -9.82513233548595E-05 0.003026776060308 -0.000110054626316 0.001768852424342 -0.000133661232237
-0.000482185804678 7.38899760184169E-05 -0.000110054626316 7.5498754980889E-05 0.000592240430994 6.75948811060119E-05
-0.001179234949561 0.000588305996674 0.001768852424342 0.000592240430994 0.007743715858553 0.000600109299635
-0.000466448067397 6.60386099950961E-05 -0.000133661232237 6.75948811060119E-05 0.000600109299635 8.1828855127665E-05
resulting Delta vector, deflection is in ft for consistent units:
Code:
0.416666666666683
-8.74300631892311E-16
0.416666666666678
-9.22872889219661E-16
0.416666666666669
-9.5062846483529E-16
From spring definition we know P=k*delta --> K=10 kip/in * .416666666 ft * 12 in / ft = 50 kips @ each spring
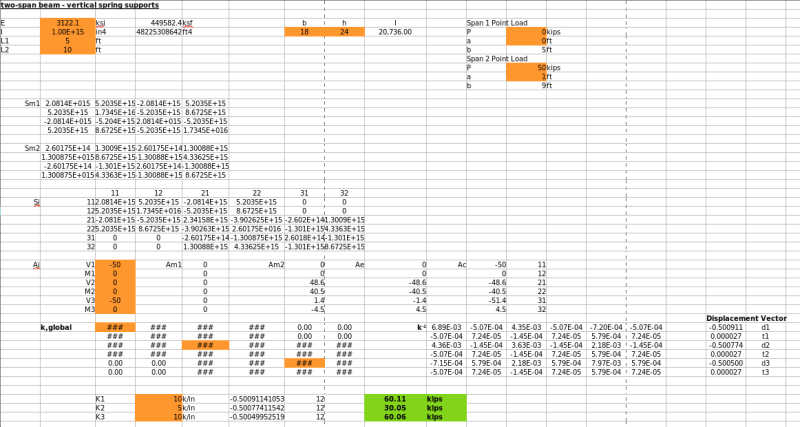
Setting the central spring to K=5 kip/in
k,global becomes:
Code:
43279.9104 107899.776 -43159.9104 107899.776 0 0
107899.776 359665.92 -107899.776 179832.96 0 0
-43159.9104 -107899.776 48614.8992 -80924.832 -5394.9888 26974.944
107899.776 179832.96 -80924.832 539498.88 -26974.944 89916.48
0 0 -5394.9888 -26974.944 5514.9888 -26974.944
0 0 26974.944 89916.48 -26974.944 179832.96
and the Delta vector becomes:
Code:
0.524735252368115
-0.003001347487258
0.509127576229035
-0.003361910708932
0.470700959517384
-0.004083037152281
Which produces the following reactions:
R1 = K1*delta1 = 10 kip/in * 0.52473... ft * 12 in/ft = 62.9682 kips
R2 = K2*delta2 = 5 kip/in * 0.50912.... ft * 12 in/ft = 30.5477 kips
R3 = K3*delta3 = 10 kip/in * 0.47070... ft * 12 in/ft = 56.4841 kips
My Personal Open Source Structural Applications:
Open Source Structural GitHub Group:

![[ponder] [ponder] [ponder]](/data/assets/smilies/ponder.gif)